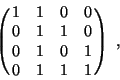
Рис. 3.11
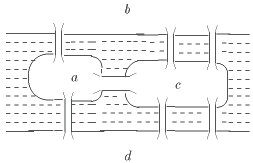
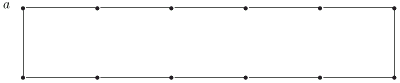
Одной из первых задач теории графов, возникшей в трудах выдающегося математика ХVIII в. Л.Эйлера, была задача о кенигсбергских мостах. Город Кенигсберг (Калининград) расположен на реке, через которую имеется семь мостов (рис. 3.11).


Популярной головоломкой среди жителей города была такая: как обойти все мосты, проходя по каждому не более одного раза ? На языке графов эта задача формулируется так: можно ли в мультиграфе, показанном на рис. 3.12, обойти все ребра, проходя по каждому ровно один раз ?
Эйлеровым циклом (цепью) в мультиграфе ![]() называется цикл (цепь), содержащий все ребра мультиграфа.
(Напомним, что, согласно определению, каждое ребро может входить
в цепь не более одного раза).
называется цикл (цепь), содержащий все ребра мультиграфа.
(Напомним, что, согласно определению, каждое ребро может входить
в цепь не более одного раза).
В одно время были распространены головоломки на тему: можно ли данный рисунок выполнить, не отрывая карандаша от бумаги и не проводя никакую линию дважды ? Это тоже задача об эйлеровом цикле; она имеет практическое приложение, как задача минимизации холостого хода пера графопостроителя.
Теорема.Мультиграф обладает эйлеровым циклом в том и только в том случае, когда он связный и все его вершины имеют четные степени.
Необходимость. Пусть мультиграф ![]() обладает
эйлеровым циклом. Поскольку в этот цикл входят все ребра мультиграфа,
то в нем встречаются и все его вершины. Следовательно,
любые две вершины соединены цепью.
обладает
эйлеровым циклом. Поскольку в этот цикл входят все ребра мультиграфа,
то в нем встречаются и все его вершины. Следовательно,
любые две вершины соединены цепью.
Рассмотрим произвольную
вершину ![]() и выделим все ее вхождения в эйлеров цикл:
и выделим все ее вхождения в эйлеров цикл:
Достаточность. Покажем, что если мультиграф связный
и степени всех вершин четны, то он обладает эйлеровым циклом.
Доказательство будем вести индукцией по числу ![]() ребер в мультиграфе.
ребер в мультиграфе.
Имеется всего один мультиграф с ![]() удовлетворяющий
условиям теоремы (рис. 3.13), и он, очевидно, обладает эйлеровым циклом.
удовлетворяющий
условиям теоремы (рис. 3.13), и он, очевидно, обладает эйлеровым циклом.
Предположим, что теорема верна для всех мультиграфов с числом
ребер, меньшим ![]() и рассмотрим мультиграф
и рассмотрим мультиграф ![]() с
с ![]() ребрами.
Будем строить обход ребер мультиграфа
ребрами.
Будем строить обход ребер мультиграфа ![]() в достаточной степени
произвольно, следя лишь за тем, чтобы не проходить ребро
дважды: начнем с произвольно выбранной вершины
в достаточной степени
произвольно, следя лишь за тем, чтобы не проходить ребро
дважды: начнем с произвольно выбранной вершины ![]() возьмем
какое-нибудь ребро, инцидентное вершине
возьмем
какое-нибудь ребро, инцидентное вершине ![]() отметим его как
пройденное и перейдем в другой конец этого ребра. В дальнейшем
действуем однотипно: попав в некоторую вершину, выбираем наудачу
одно из инцидентных этой вершине непройденных ребер, отмечаем
его и переходим в другой его конец. На некотором шаге такого
построения обнаружится, что дальше двигаться нельзя: все
ребра, инцидентные вершине, до которой дошло построение, отмечены
как пройденные. Утверждается, что такой вершиной может
быть только начальная вершина
отметим его как
пройденное и перейдем в другой конец этого ребра. В дальнейшем
действуем однотипно: попав в некоторую вершину, выбираем наудачу
одно из инцидентных этой вершине непройденных ребер, отмечаем
его и переходим в другой его конец. На некотором шаге такого
построения обнаружится, что дальше двигаться нельзя: все
ребра, инцидентные вершине, до которой дошло построение, отмечены
как пройденные. Утверждается, что такой вершиной может
быть только начальная вершина ![]() Это очевидным образом
вытекает иэ того, что степень каждой вершины четная.
Это очевидным образом
вытекает иэ того, что степень каждой вершины четная.
Таким образом, пройденные ребра образуют некоторый цикл, обозначим его ![]() Если этот цикл содержит все ребра мультиграфа
Если этот цикл содержит все ребра мультиграфа ![]() то он и
есть эйлеров. Рассмотрим, как действовать в случае, когда остались
непройденные ребра. Удалив из
то он и
есть эйлеров. Рассмотрим, как действовать в случае, когда остались
непройденные ребра. Удалив из ![]() все пройденные ребра,
получим мультиграф
все пройденные ребра,
получим мультиграф ![]() в котором по-прежнему все вершины
имеют четную степень, но он будет несвязным. Пусть
в котором по-прежнему все вершины
имеют четную степень, но он будет несвязным. Пусть
![]() -- компоненты связности
-- компоненты связности ![]() имеющие более
одной вершины. Так как каждая из компонент представляет собой связный
мультиграф с четными степенями вершин и с числом ребер, меньшим
имеющие более
одной вершины. Так как каждая из компонент представляет собой связный
мультиграф с четными степенями вершин и с числом ребер, меньшим ![]() то по предположению индукции она обладает эйлеровым циклом.
Обозначим эйлеровы циклы компонент
то по предположению индукции она обладает эйлеровым циклом.
Обозначим эйлеровы циклы компонент
![]() 3аметим также, что первоначально построенный цикл
3аметим также, что первоначально построенный цикл ![]() заходит
в каждую из компонент, т.е. в каждом мультиграфе
заходит
в каждую из компонент, т.е. в каждом мультиграфе ![]() можно найти
вершину
можно найти
вершину ![]() через которую проходит цикл
через которую проходит цикл ![]() Это вытекает
из того, что после добавления к несвязному мультиграфу
Это вытекает
из того, что после добавления к несвязному мультиграфу ![]() ребер
цикла
ребер
цикла ![]() получается связный мультиграф
получается связный мультиграф ![]()
Эйлеров цикл мультиграфа ![]() строится теперь следующим образом:
в цикле
строится теперь следующим образом:
в цикле ![]() находим первую вершину
находим первую вершину ![]() входящую в одну из
компонент
входящую в одну из
компонент
![]() Включаем в цикл
Включаем в цикл ![]() цикл
цикл ![]() (то есть заменяем вершину
(то есть заменяем вершину ![]() последовательностью
последовательностью
![]() ) В оставшейся части цикла
) В оставшейся части цикла ![]() снова находим первую вершину
снова находим первую вершину ![]() входящую в одну из компонент и
включаем цикл для этой компоненты. Так действуем пока не будут включены
все эйлеровы циклы компонент.
входящую в одну из компонент и
включаем цикл для этой компоненты. Так действуем пока не будут включены
все эйлеровы циклы компонент.
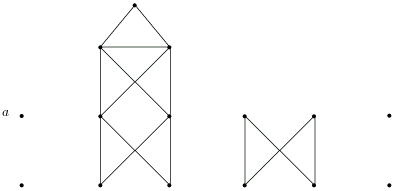
Пример. В графе, показанном на рис. 3.14, степени всех вершин четные.
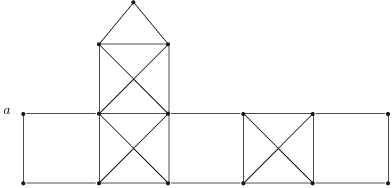
Допустим, что на первом этапе рассмотренного выше алгоритма построен цикл, показанный на рис. 3.15.
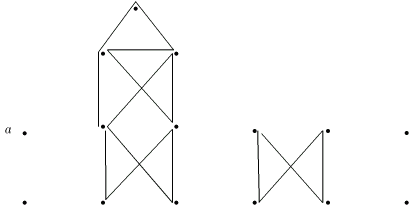
Непройденные ребра образуют несвязный граф, показанный на pис. 3.16.
Строим эйлеровы циклы компонент (рис. 3.17).
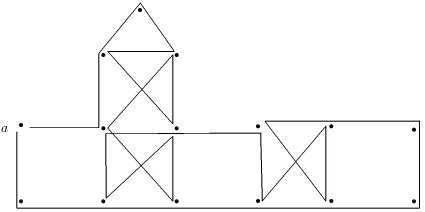
Дополнения к теореме
1. Если связный мультиграф имеет ровно две вершины с нечетной степенью, то он обладает эйлеровой цепью.
Действительно, временно добавим к мультиграфу новое ребро, соединяющее вершины с нечетной степенью; в результате степени всех вершин станут четными. Построим в новом графе эйлеров цикл, а затем удалим добавленное ребро: цикл разорвется и станет цепью. Этa цепь начинается и заканчивается в вершинах нечетной степени.
2. В общем случае число вершин мультиграфа, имеющих нечетную
степень, равно ![]() (оно всегда четно). Все ребра такого
мультиграфа можно включить в
(оно всегда четно). Все ребра такого
мультиграфа можно включить в ![]() цепей. Другими словами, мультиграф
можно нарисовать,
цепей. Другими словами, мультиграф
можно нарисовать, ![]() раз отрывая карандаш от бумаги.
Обоснование этого факта такое же, как и выше: добавляем новые
раз отрывая карандаш от бумаги.
Обоснование этого факта такое же, как и выше: добавляем новые
![]() ребер, соединяющие пары вершин с нечетной степенью, строим
эйлеров цикл, удаляем новые ребра.
ребер, соединяющие пары вершин с нечетной степенью, строим
эйлеров цикл, удаляем новые ребра.
Пусть задан граф
![]() Ребро графа, через которое
проходит хотя бы один цикл, назовем цикловым ребром. Ребро,
которое не входит ни в один цикл, будем называть перешейком.
Ребро графа, через которое
проходит хотя бы один цикл, назовем цикловым ребром. Ребро,
которое не входит ни в один цикл, будем называть перешейком.
Пример. В графе, изображенном на рис.3.19, ребра ![]() и
и ![]() -- перешейки,
остальные ребра цикловые.
-- перешейки,
остальные ребра цикловые.
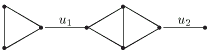
Лемма. При удалении из связного графа циклового ребра он остается связным. При удалении из связного графа перешейка граф распадается на две компоненты.
Действительно, если удаляемое ребро ![]() цикловое, то
после его удаления вершины
цикловое, то
после его удаления вершины ![]() и
и ![]() по-прежнему можно соединить
цепью -- остатком цикла, в который входило ребро
по-прежнему можно соединить
цепью -- остатком цикла, в который входило ребро ![]() Отсюда
вытекает, что и любые две вершины графа после удаления ребра
Отсюда
вытекает, что и любые две вершины графа после удаления ребра
![]() остаются связанными цепью. Напротив, если
остаются связанными цепью. Напротив, если ![]() -- перешеек,
то после его удаления вершины
-- перешеек,
то после его удаления вершины ![]() и
и ![]() нельзя связать
цепью, иначе эта цепь вместе с ребром
нельзя связать
цепью, иначе эта цепь вместе с ребром ![]() образует
цикл в исходном графе. С другой стороны, каждая вершина
остается связанной либо с вершиной
образует
цикл в исходном графе. С другой стороны, каждая вершина
остается связанной либо с вершиной ![]() либо с вершиной
либо с вершиной ![]()
Следствие. При удалении из графа циклового ребра число связных компонент графа не изменяется. При удалении перешейка число связных компонент графа увеличивается на единицу.
Пусть дан граф
![]() и пусть
и пусть ![]() имеет
имеет ![]() компонент связности.
компонент связности.
Величина
![]() называется цикломатическим числом графа.
называется цикломатическим числом графа.
Теорема. Для любого графа цикломатическое число неотрицательно:
Доказательство. Будем удалять из графа по одному
ребру и следить за изменением величины ![]() Параметры исходного
графа обозначим
Параметры исходного
графа обозначим ![]() те же величины после удаления
ребра обозначим
те же величины после удаления
ребра обозначим ![]()
В процессе удаления ребер могут представиться два случая:
а) удаляемое ребро цикловое. Тогда
б) удаляемое ребро -- перешеек. В этом случае
Итак, при удалении ребра величина ![]() либо не изменяется,
либо уменьшается на единицу. После удаления всех ребер
получится пустой граф, в котором
либо не изменяется,
либо уменьшается на единицу. После удаления всех ребер
получится пустой граф, в котором
![]() т.е.
т.е.
![]() Следовательно, в исходном графе
Следовательно, в исходном графе
![]()
Доказательство теоремы указывает на связь цикломатического
числа с наличием циклов в графе. Действительно, если
![]() то в графе есть, по крайней мере, один цикл. При удалении циклового
ребра некоторые циклы разрываются, и это приводит к уменьшению
то в графе есть, по крайней мере, один цикл. При удалении циклового
ребра некоторые циклы разрываются, и это приводит к уменьшению ![]() Если продолжать удаление ребер, то в конце концов разрываются все циклы и
Если продолжать удаление ребер, то в конце концов разрываются все циклы и
![]() становится равным нулю.
После этого
становится равным нулю.
После этого ![]() уже не изменяется, так как все ребра стали
перешейками.
уже не изменяется, так как все ребра стали
перешейками.
Пример. Пусть требуется связать несколько населенных пунктов сетью дорог или телефонной сетью, вообще как-то связать друг с другом. Предлагаемый проект показан на рис. 3.20,а.

В дальнейшем потребовалось удешевить проект, в результате некоторые связи были исключены (рис.3.20,б и 3.20,в).
В графе на рис. 3.20,в больше уже никакие связи исключить нельзя, иначе граф перестанет быть связным и поставленная задача не будет решена. Такого рода графы называются деревьями.
Деревом называется связный граф без циклов. В следующей теореме перечисляются свойства деревьев, каждое из этих свойств полностью характеризует дерево.
Теорема.Следующие определения дерева эквивалентны:
а) дерево - это связный граф без циклов;
б ) дерево - это связный граф, в котором каждое ребро является перешейком;
в) дерево - это связный граф, цикломатическое число которого равно нулю;
г) дерево - это граф, в котором для любых двух вершин имеется ровно одна соединяющая их цепь.
Перечисленные утверждения несложным образом выводятся одно
из другого по схеме
![]()
В силу свойства в) имеем ![]() или
или ![]() т.е. в любом дереве число ребер на единицу меньше числа вершин.
т.е. в любом дереве число ребер на единицу меньше числа вершин.
Рис. 3.21 некоторым образом объясняет название "дерево".
Выделим в дереве некоторую вершину ![]() (корень). Поскольку
примыкающие к ней ребра -- перешейки, то после удаления любого
из них от дерева отделяется компонента. На рисунке они
обозначены
(корень). Поскольку
примыкающие к ней ребра -- перешейки, то после удаления любого
из них от дерева отделяется компонента. На рисунке они
обозначены
![]() Каждая из этих компонент также является
деревом.
Каждая из этих компонент также является
деревом.
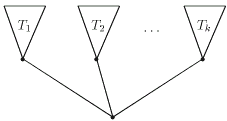
Рассмотрим связный граф и будем удалять из него по одному цикловые
ребра до тех пор, пока их не останется.
В результате получится дерево
![]() такое, что:
такое, что:
1) ![]() т.е. множество вершин дерева
т.е. множество вершин дерева ![]() совпадает
с множеством вершин графа
совпадает
с множеством вершин графа ![]() ;
;
2)
![]() т.е.каждое ребро дерева является в то же время ребром графа
т.е.каждое ребро дерева является в то же время ребром графа ![]()
Любое дерево ![]() удовлетворяющее условиям 1) и 2), называется
остовным деревом графа
удовлетворяющее условиям 1) и 2), называется
остовным деревом графа ![]()
Так как удаление цикловых ребер можно вести разными способами, то один и тот же граф имеет, вообще говоря, много остовных деревьев.
Пример.
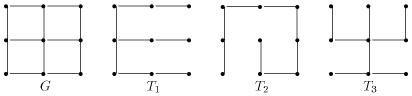
На рис.3.22 показан граф ![]() и три его остовных дерева.
и три его остовных дерева.
Пусть в графе ![]() выделено остовное дерево
выделено остовное дерево ![]() Ребра
графа, не вошедшие в
Ребра
графа, не вошедшие в ![]() будем называть хордами дерева
будем называть хордами дерева ![]()
Лемма.Каковы бы ни были остовное дерево ![]() и хорда
и хорда ![]() этого дерева,
в графе
этого дерева,
в графе ![]() существует единственный цикл, содержащий хорду
существует единственный цикл, содержащий хорду ![]() и не содержащий других хорд.
и не содержащий других хорд.
Доказательство. Пусть
![]() В дереве
В дереве ![]() имеется единственная цепь, соединяющая вершины
имеется единственная цепь, соединяющая вершины ![]() и
и ![]() Присоединяя к этой цепи ребро
Присоединяя к этой цепи ребро ![]() получаем требуемый цикл.
получаем требуемый цикл.
Пусть
![]() -- нагруженный граф. Требуется построить
остовное дерево
-- нагруженный граф. Требуется построить
остовное дерево ![]() графа
графа ![]() сумма длин ребер которого
минимальна.
сумма длин ребер которого
минимальна.
Этой задаче можно дать такую интерпретацию: ![]() пунктов на
местности нужно связать сетью дорог, трубопроводов или линий телефонной связи.
Для каждой пары пунктов
пунктов на
местности нужно связать сетью дорог, трубопроводов или линий телефонной связи.
Для каждой пары пунктов ![]() и
и ![]() задана стоимость их
соединения -- это и есть "длина"
задана стоимость их
соединения -- это и есть "длина" ![]() ребра
ребра ![]() в данном
случае. Требуется построить связывающую сеть минимальной стоимости, ее называют
кратчайшей связывающей сетью.
в данном
случае. Требуется построить связывающую сеть минимальной стоимости, ее называют
кратчайшей связывающей сетью.
Очевидно, что кратчайшая связывающая сеть будет остовным деревом графа ![]() при этом среди всех остовных деревьев она будет иметь минимальную сумму длин
входящих в нее ребер.
при этом среди всех остовных деревьев она будет иметь минимальную сумму длин
входящих в нее ребер.
Алгоритм построения кратчайшей связывающей сети состоит из ![]() шагов, на каждом шаге присоединяется одно ребро.
Правило для выбора этого ребра следующее: среди еще не выбранных
ребер берется самое короткое, не образующее цикла с уже
выбранными ребрами.
шагов, на каждом шаге присоединяется одно ребро.
Правило для выбора этого ребра следующее: среди еще не выбранных
ребер берется самое короткое, не образующее цикла с уже
выбранными ребрами.
Пример. В матрице ![]() элемент, стоящий в
элемент, стоящий в ![]() -й строке
и
-й строке
и ![]() -м столбце, указывает в условных единицах затраты,
необходимие для того, чтобы связать пункт
-м столбце, указывает в условных единицах затраты,
необходимие для того, чтобы связать пункт ![]() с пунктом
с пунктом ![]() :
:

3адача заключается в том, чтобы с наименьшими затратами связать все пункты друг с другом.
Применение сформулированного выше алгоритма выглядит так.
В матрице ![]() отыскивается минимальный элемент. Он вычеркивается
из матрицы, а соответствующее ему ребро зачисляется в сеть, если
при этом не образуется циклов. Эти действия повторяются. Таким
образом, на первых пяти шагах работы алгоритма будут выбраны
ребра
отыскивается минимальный элемент. Он вычеркивается
из матрицы, а соответствующее ему ребро зачисляется в сеть, если
при этом не образуется циклов. Эти действия повторяются. Таким
образом, на первых пяти шагах работы алгоритма будут выбраны
ребра
![]()
Из оставшихся ребер минимальную длину имеет ребро ![]() но в сеть оно не включается, так как образует цикл с уже выбранными ребрами.
На последующих этапах алгоритма в сеть будут включены ребра
но в сеть оно не включается, так как образует цикл с уже выбранными ребрами.
На последующих этапах алгоритма в сеть будут включены ребра
![]() и
и ![]()
Для обоснования алгоритма предположим, что дерево ![]() которое
он строит, состоит из ребер
которое
он строит, состоит из ребер
Пример. Слово
![]() задает исходный граф
задает исходный граф ![]() слово
слово
![]() -- его пустой остовный подграф.
-- его пустой остовный подграф.
Двоичные слова длины ![]() образуют векторное пространство
над полем из двух элементов
образуют векторное пространство
над полем из двух элементов
![]() в котором операции
определены так
в котором операции
определены так
В силу биекции (3.4) мы можем не различать остовные подграфы и соответствующие
двоичные слова и говорить о пространстве остовных подграфов
графа ![]() -- это векторное пространство размерности
-- это векторное пространство размерности ![]() над
полем из двух элементов. Сумму двух остовных подграфов
над
полем из двух элементов. Сумму двух остовных подграфов ![]() и
и
![]() будем обозначать
будем обозначать
![]() В силу указанной биекции
это остовный подграф, задаваемый словом
В силу указанной биекции
это остовный подграф, задаваемый словом
![]() он состоит из всех тех ребер, которые входят ровно в один из подграфов-слагаемых.
Что касается операции умножения на скаляр, то она в рассматриваемом пространстве
тривиальна: умножение на 1 не меняет подграф, умножение на 0 дает пустой подграф.
он состоит из всех тех ребер, которые входят ровно в один из подграфов-слагаемых.
Что касается операции умножения на скаляр, то она в рассматриваемом пространстве
тривиальна: умножение на 1 не меняет подграф, умножение на 0 дает пустой подграф.
В качестве базиса в пространстве остовных подграфов можно
взять совокупность из ![]() однореберных подграфов. Им соответствуют
двоичные слова с одной единицей.
однореберных подграфов. Им соответствуют
двоичные слова с одной единицей.
В пространстве остовных подграфов выделим подпространство, содержащее все циклы графа.
Остовный подграф называется квазициклом, если степень каждой его вершины четна.
Всякий цикл является квазициклом. Приставка "квази" означает "как бы", "похожий на". Из теоремы об эйлеровом цикле следует, что кроме циклов, в число квазициклов входят подграфы, состоящие из нескольких компонент, каждая из которых является циклом (необязательно простым). Отметим также, что пустой подграф является квазициклом.
Лемма. Сумма двух квазициклов является квазициклом.
Доказательство. Пусть ![]() и
и ![]() -- квазициклы,
покажем, что
-- квазициклы,
покажем, что
![]() тоже квазицикл. Рассмотрим произвольную
вершину графа
тоже квазицикл. Рассмотрим произвольную
вершину графа ![]() Допустим, что в квазицикле
Допустим, что в квазицикле ![]() к этой вершине
примыкает
к этой вершине
примыкает ![]() ребер, в квазицикле
ребер, в квазицикле
![]() ребер и пусть
ребер и пусть
![]() ребер из них общие для
ребер из них общие для ![]() и
и ![]() В сумму
В сумму
![]() войдут
войдут ![]() ребер, входящих
только в
ребер, входящих
только в ![]() и
и ![]() ребер, входящих только в
ребер, входящих только в ![]() всего --
всего --
![]() ребер.
Следовательно, степень рассматриваемой вершины будет
четной, т.е.
ребер.
Следовательно, степень рассматриваемой вершины будет
четной, т.е.
![]() -- квазицикл.
-- квазицикл.
Лемма показывает, что совокупность квазициклов так же является векторным
пространством над полем ![]() Оно называется пространством циклов графа
Оно называется пространством циклов графа ![]() Ясно, что пространство циклов
является подпространством в векторном пространстве остовных подграфов.
Ясно, что пространство циклов
является подпространством в векторном пространстве остовных подграфов.
В следующей теореме находится размерность и базис этого подпространства.
Основная теорема.В графе ![]() с цикломатическим числом
с цикломатическим числом ![]() можно найти
можно найти ![]() простых циклов
простых циклов
![]() со следующими свойствами:
со следующими свойствами:
1) любой квазицикл ( в частности, любой цикл ) можно представить
в виде суммы некоторых циклов
![]() ;
;
2) циклы
![]() независимы, т.е. никакой из них
нельзя выразить в виде суммы через остальные.
независимы, т.е. никакой из них
нельзя выразить в виде суммы через остальные.
Система векторов, удовлетворяющая условиям
1) и 2), называется базисом, количество векторов в базисе называют
размерностью соответствующего пространства. Поэтому совокупность
циклов
![]() носит название системы базисных
циклов графа
носит название системы базисных
циклов графа ![]() а основную теорему можно сформулировать так:
а основную теорему можно сформулировать так:
Доказательство будем вести для связного графа ![]() (система базисных циклов произвольного графа получается объединением
систем базисных циклов компонент). Так как
(система базисных циклов произвольного графа получается объединением
систем базисных циклов компонент). Так как ![]() связный, то
связный, то
![]()
Выделим в графе ![]() какое-либо остовное дерево
какое-либо остовное дерево ![]() В него
входит
В него
входит ![]() ребро графа, остальные
ребро графа, остальные
![]() ребер графа
являются хордами этого дерева. 3анумеруем ребра графа так, чтобы
первые
ребер графа
являются хордами этого дерева. 3анумеруем ребра графа так, чтобы
первые ![]() номеров получили хорды, а остальные -- ребра дерева.
Для каждой хорды
номеров получили хорды, а остальные -- ребра дерева.
Для каждой хорды ![]() выполним следующее построение: присоединим
хорду к дереву
выполним следующее построение: присоединим
хорду к дереву ![]() и построим цикл
и построим цикл ![]() состоящий из хорды
состоящий из хорды ![]() и цепи в дереве, соединяющей концы хорды. Построенные таким образом
циклы
и цепи в дереве, соединяющей концы хорды. Построенные таким образом
циклы
![]() и образуют систему базисных циклов.
и образуют систему базисных циклов.
Чтобы в этом убедиться, выпишем для каждого из базисных циклов соответствующее двоичное слово:

Никакой цикл ![]() нельзя выразить через остальные:
соответствующее слово
нельзя выразить через остальные:
соответствующее слово
![]() имеет единицу в
имеет единицу в ![]() -м разряде,
а у остальных слов в этом разряде стоит нуль.
-м разряде,
а у остальных слов в этом разряде стоит нуль.
Рассмотрим далее произвольный квазицикл ![]() и покажем, как его
представить в виде суммы базисных циклов. Пусть
и покажем, как его
представить в виде суммы базисных циклов. Пусть ![]() слово, соответствующее
слово, соответствующее ![]() Среди первых
Среди первых ![]() разрядов этого
слова найдем все те, которые равны единице.
Пусть
разрядов этого
слова найдем все те, которые равны единице.
Пусть
![]() -- номера этих разрядов. Рассмотрим
квазицикл
-- номера этих разрядов. Рассмотрим
квазицикл
![]() Он имеет единицы в тех же разрядах среди первых
Он имеет единицы в тех же разрядах среди первых ![]() что и рассматриваемый квазицикл
что и рассматриваемый квазицикл ![]() Двоичные слова
Двоичные слова
![]() и
и
![]() совпадают в первых
совпадают в первых ![]() разрядах,
следовательно, слово
разрядах,
следовательно, слово
![]() в первых
в первых ![]() разрядах
имеет нули, то есть квазицикл
разрядах
имеет нули, то есть квазицикл
![]() составлен только из ребер дерева. Учитывая, что любой квазицикл либо пустой,
либо имеет компоненту, являющуюся циклом, и тот факт, что в дереве нет циклов,
заключаем, что квазицикл
составлен только из ребер дерева. Учитывая, что любой квазицикл либо пустой,
либо имеет компоненту, являющуюся циклом, и тот факт, что в дереве нет циклов,
заключаем, что квазицикл
![]() пустой или
пустой или
![]() Отсюда
Отсюда ![]() т.е.
т.е.
![]()
Теорема доказана.
Пример. Построим систему базисных циклов для графа ![]() показанного на рис. 3.22.
показанного на рис. 3.22.
Выделим остовное дерево ![]() (рис. 3.23,а).
(рис. 3.23,а).

Присоединяя к дереву по очереди хорды
![]() получаем 4 базисных цикла, показанные на рис.3.24.
получаем 4 базисных цикла, показанные на рис.3.24.
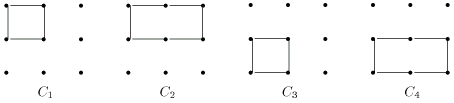
Для того же графа можно построить систему базисных циклов, основываясь
на дереве ![]() (рис.3.23,б). Действуя аналогично предыдущему, получаем
базисные циклы, показанные на рис.3.25.
(рис.3.23,б). Действуя аналогично предыдущему, получаем
базисные циклы, показанные на рис.3.25.
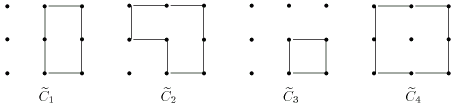
Циклы одной из систем можно выразить как линейные комбинации циклов
из другой системы. Для этого надо действовать как указано в доказательстве
основной теоремы. Например, цикл
![]() содержит хорды
содержит хорды
![]() и
и ![]() дерева
дерева ![]() поэтому
поэтому
![]() В итоге получим
В итоге получим

Это знакомые по курсу линейной алгебры формулы перехода к новому базису
в векторном пространстве (в данном примере 4-мерном). Матрица перехода