2.3. Рекуррентные соотношения


Для подсчета дискретных объектов широко применяется техника рекуррентных соотношений и производящих функций. Поясним ее сущность на примерах.

Пример 1. Рассмотрим следующую задачу: подсчитать количество двоичных слов длины $ \;n,\;$ в которых единицы не могут стоять на соседних местах. Будем называть такие слова правильными и обозначим через $ \;A_n\;$ число правильных слов длины $ \;n.\;$ Разобъем множество правильных слов длины $ \;n\;$ на два класса: слова, оканчивающиеся на ноль и слова, оканчивающиеся на единицу. Количество слов в этих классах обозначим $ \;A_n^{(0)}\;$ и $ \;A_n^{(1)},\;$ соответственно. Имеем по правилу сложения

$\displaystyle \;A_n=A_n^{(0)}+A_n^{(1)}\;.\eqno{(2.5)}$

Очевидно, что у слова, оканчивающегося на ноль, первые $ \;n-1\;$ символ образуют правильное слово длины $ \;n-1,\;$ или, другими словами, имеется биекция между множеством правильных слов длины $ \;n,\;$ оканчивающихся на ноль, и множеством всех правильных слов длины $ \;n-1.\;$ Следовательно, $ \;A_n^{(0)}=A_{n-1}.$

Если правильное слово длины $ \;n\;$ оканчивается на единицу, то предыдущий символ этого слова ($ \;n-1$-й) должен быть нулем, а первые $ \;n-2\;$ символа должны образовывать правильное слово длины $ \;n-2.\;$ Как и в предыдущем рассуждении, снова имеем биекцию между множеством правильных слов длины $ \;n,\;$ оканчивающихся на единицу и множеством всех правильных слов длины $ \;n-2.\;$ Следовательно, $ \;A_n^{(1)}=A_{n-2}.\;$ Подставляя в (2.5), получаем соотношение

$\displaystyle A_n=A_{n-1}+A_{n-2}\;.$

Оно называется рекуррентным, в переводе -- возвратным, так как для подсчета интересующей нас величины для некоторого $ \;n\;$ нужно возвратиться к предыдущим значениям этой величины. В общем случае рекуррентное соотношение имеет вид

$\displaystyle A_n=F(A_{n-1},A_{n-2},\ldots A_{n-k})\;.\eqno{(2.6)}$

Рекуррентное соотношение в известном смысле решает задачу подсчета, но требует для данного $ \;n\;$ вычисления всех предыдущих величин. Например, если нам нужно знать количество правильных слов из 10 символов, то его можно найти, заполняя следующую таблицу

#&#& #&#& #&#& #&#& #&#& #&#& #&#& #&#& #&#& #&#& #&#& #&#
&& $ n$ && 1 && 2 && 3 && 4 && 5 && 6 && 7 && 8 && 9 && 10 &
&& $ A_n$ && 2 && 3 && 5 && 8 && 13 && 21 && 34 && 55 && 89 && 144 &

(Первые два значения находятся непосредственно, а затем вычисляем $ \;A_3=A_2+A_1\;,\;A_4=A_3+A_2\;,\ldots\;)$


Пример 2.

Пусть $ \;''\circ''\;$ обозначает некоторую бинарную операцию, рассмотрим выражение

$\displaystyle a_1\circ a_2\circ\ldots\circ a_n\;.\eqno{(2.7)}$

Если операция $ \;''\circ''\;$ неассоциативна, то результат вычисления выражения (2.7) зависит от расстановки скобок. Сколько имеется различных способов расстановки скобок в выражениии (2.7)?

Замечание. Как пример неассоциативной операции можно привести векторное произведение. Другой удивительный пример: $ \;''\circ''\;$ -- обычное сложение или умножение, но выполняемое на компьютере. В силу того, что представление каждого числа в памяти компьютера ограничено определенным количеством разрядов, при выполнении каждой операции возникает погрешность и суммарный результат этих погрешностей зависит от расстановки скобок. Пусть, например, $ \;\varepsilon\;$ максимальное положительное число такое, что $ \;1+\varepsilon=1.\;$ Это так называемый машинный ноль. Тогда $ \;(1+\varepsilon)+\varepsilon=1,\;$ в то время как $ \;1+(\varepsilon+\varepsilon)=1+2\,\varepsilon\not=1.$

Обозначив число всевозможных способов расстановки скобок через $ \;D_n,\;$ имеем

$\displaystyle D_1$ $\displaystyle =D_2=1$    
$\displaystyle D_3$ $\displaystyle =2\quad (a_1\circ a_2)\circ a_3\;,\;a_1\circ(a_2\circ a_3)$    
$\displaystyle D_4$ $\displaystyle =5\quad ((a_1\circ a_2)\circ a_3)\circ a_4\;,\;(a_1\circ(a_2\circ a_3))\circ a_4\;,\;(a_1\circ a_2)\circ (a_3\circ a_4)\;,$    
  $\displaystyle \qquad\quad a_1\circ ((a_2\circ a_3)\circ a_4)\;,\;a_1\circ (a_2\circ (a_3\circ a_4))\;.$    

В случае произвольного $ \;n\;$ разобьем все способы расстановки скобок на классы, включив в $ \;k$-й класс способы, при которых сначала вычисляется "произведение" первых $ \;k\;$ и последних $ \;n-k\;$ операндов (с какой-то расстановкой скобок), а потом вычисляется их произведение

$\displaystyle (a_1\circ \ldots\circ a_k)\circ (a_{k+1}\circ \ldots\circ a_n)\;.\eqno{(2.8)}$

( $ \;k=1,2,\ldots ,n-1\;.$)

Согласно определению, количество способов расстановки скобок для вычисления "произведения" первых $ \;k\;$ операндов равно $ \;D_k,\;$ последних $ \;n-k\;$ -- $ \;D_{n-k},\;$ следовательно, число расстановок скобок вида (2.8) равно $ \;D_k\cdot D_{n-k}.\;$ Суммируя по всевозможным $ \;k\;$ (правило сложения !), находим

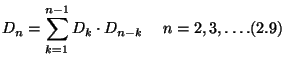
$\displaystyle D_n=\sum_{k=1}^{n-1} D_k\cdot D_{n-k}\;\quad n=2,3,\ldots.\eqno{(2.9)}$

Например, $ \;D_5=D_1D_4+D_2D_3+D_3D_2+D_4D_1=1\cdot 5+1\cdot 2+2\cdot 1+5\cdot 1=14\;$


Хотя рекуррентное соотношение в принципе решает задачу подсчета, в ряде случаев желательно иметь выражение для искомой величины в явном виде. Такое явное выражение можно получить для решений одного класса рекуррентных соотношений -- линейных рекуррентных соотношений с постоянными коэффициентами.

Решение линейных рекуррентных соотношений

Пусть функция $ \;F\;$ в общем определении (2.6) является линейной,

$\displaystyle A_n=\alpha_1\,A_{n-1}+\alpha_2\,A_{n-2}+\ldots +\alpha_k\,A_{n-k}\;,\quad n=k,k+1,\ldots\;,$

$\displaystyle \alpha_1,\alpha_2,\ldots,\alpha_k\,\hbox{--- заданные числа}\;.\eqno{(2.10)}$

Тогда соотношение (2.10) называют линейным рекуррентным соотношением $ \;k$-го порядка: (Более точно надо бы говорить "линейное рекуррентное соотношение с постоянными коэффициентами".)

Соотношение (2.10) мы будем далее рассматривать как уравнение (относительно неизвестной функции $ \;A(n)=A_n\;$ ) и каждую последовательность

$\displaystyle \tilde A=(A_0,A_1,\ldots ,A_n,\ldots )\;,$

для которой выполнены соотношения (2.10), будем называть решением рекуррентного соотношения.

Основные моменты теории линейных рекуррентных соотношений произвольного порядка можно понять на примере уравнений второго порядка -- общий случай сложней только в обозначениях. Поэтому, далее исследуем подробно уравнения второго порядка

$\displaystyle A_n=\alpha_1\,A_{n-1}+\alpha_2\,A_{n-2}\;,\quad n=2,3,\ldots\;\;,\eqno{(2.11)}$

делая необходимые замечания для общего случая.
Описание совокупности решений

Лемма 1.Пусть

$\displaystyle \tilde A=(A_0,A_1,\ldots ,A_n,\ldots )\;$

является решением рекуррентного соотношения (2.11), а $ \;C\;$ -- любое число. Тогда последовательность

$\displaystyle C\tilde A=(C\,A_0,C\,A_1,\ldots ,C\,A_n,\ldots )\;$

также является решением рекуррентного соотношения (2.11).

Подставив вторую последовательность в (2.11) и поделив на $ \;C,\;$ убеждаемся, что вторая последовательность является решением, поскольку решением является первая последовательность. Если $ \;C=0,\;$ то последовательность  $ \;C\tilde A\;$ состоит из одних нулей. Такая последовательность, очевидно, будет решением любого линейного рекуррентного соотношения.

Лемма 2.Пусть

$\displaystyle \tilde A=(A_0,A_1,\ldots ,A_n,\ldots )\;\;\hbox{и}\;\;\tilde B=(B_0,B_1,\ldots ,B_n,\ldots )\;-$

два решения рекуррентного соотношения (2.11).

Тогда последовательность

$\displaystyle \tilde C=\tilde A+\tilde B=(A_0+B_0\,,\,A_1+B_1\,,\ldots ,\,A_n+B_n\,,\ldots )\;$

также является решением рекуррентного соотношения (2.11).

Так как $ \;\tilde A\;\hbox{и}\;\tilde B\;$ являются решениями, то

  $\displaystyle A_n=\alpha_1\,A_{n-1}+\alpha_2\,A_{n-2}$    
  $\displaystyle B_n=\alpha_1\,B_{n-1}+\alpha_2\,B_{n-2}\;,\quad n=2,3,\ldots\;.$    

Сложив эти соотношения, убеждаемся, что $ \;\tilde C\;$ также является решением.

Из этих двух простых лемм можно сделать важный вывод. Совокупность всевозможных последовательностей

$\displaystyle \tilde A=(A_0,A_1,\ldots ,A_n,\ldots )$

вместе с операциями покоординатного сложения (как в лемме 2) и умножения на скаляр (как в лемме 1) образует векторное пространство. Из лемм 1 и 2 вытекает, что совокупность последовательностей, являющихся решениями (2.11), представляет собой подпространство этого пространства. Объемлющее пространство всевозможных последовательностей бесконечномерно, но подпространство решений линейного рекуррентного соотношения имеет конечную размерность, равную порядку уравнения.

Лемма 3.Размерность пространства решений рекуррентного соотношения (2.11) равна двум.

Для доказательства заметим, что если последовательность $ \;(A_n)\;$ удовлетворяет рекуррентному соотношению (2.11), то она полностью определяется заданием первых двух членов. Действительно, если

$\displaystyle \;A_0=a\;,\quad A_1=b\;,\eqno{(2.12)}$

то

$\displaystyle A_2$ $\displaystyle =\alpha_1\,A_1+\alpha_2\,A_0=\alpha_1\,b+\alpha_2\,a$    
$\displaystyle A_3$ $\displaystyle =\alpha_1\,A_2+\alpha_2\,A_1=\alpha_1\,(\alpha_1\,b+\alpha_2\,a)+\alpha_2\,b$    
  $\displaystyle \ldots$    

Другими словами, чтобы задать последовательность-решение, достаточно задать первые два члена последовательности. Определим базисные решения $ \;\tilde E^{(0)}\;$ и $ \;\tilde E^{(1)}\;$ так

  $\displaystyle E^{(0)}_0=1\;,\;E^{(0)}_1=0\;,\quad E^{(0)}_n=\alpha_1\,E^{(0)}_{n-1}+\alpha_2\,E^{(0)}_{n-2}\;,\; n=2,3,\ldots$    
  $\displaystyle E^{(1)}_0=0\;,\;E^{(1)}_1=1\;,\quad E^{(1)}_n=\alpha_1\,E^{(1)}_{n-1}+\alpha_2\,E^{(1)}_{n-2}\;,\; n=2,3,\ldots$    

Если имеется произвольное решение $ \;\tilde A,\;$ первые два члена которого задаются формулами (2.12), то, очевидно,

$\displaystyle \tilde A=a\,\tilde E^{(0)}+b\,\tilde E^{(1)}\;.$

Лемма 3 доказана.

Отыскание базисных решений

Итак, чтобы найти все решения уравнения (2.11) достаточно как-то отыскать два линейно независимых решения -- каждое решение будет составляться как линейная комбинация базисных.

Путь для отыскания базисных решений подсказывает рассмотрение рекуррентного соотношения первого порядка

$\displaystyle A_n=\lambda A_{n-1}\;.\eqno{(2.13)}$

Если $ \;A_0=1,\;$ то из (2.13) получаем

$\displaystyle \;A_n=\lambda^n\;,\eqno{(2.14)}$

то есть решением рекуррентного соотношения первого порядка является геометрическая прогрессия.

Будем и в общем случае искать решение рекуррентного соотношения в виде геометрической прогрессии (2.14). Подстановка (2.14) в (2.11) дает

$\displaystyle \lambda^n=\alpha_1\,\lambda^{n-1}+\alpha_2\,\lambda^{n-2}\;.$

При $ \;\lambda=0\;$ имеем нулевое решение, оно не представляет для нас интереса. Считая $ \;\lambda\not=0,\;$ поделим предыдущее соотношение на $ \;\lambda^{n-2}\;:$

$\displaystyle \lambda^2=\alpha_1\,\lambda+\alpha_2\;.\eqno{(2.15)}$

Итак, геометрическая прогрессия (2.14) является решением линейного рекуррентного соотношения (2.11), если знаменатель прогрессии $ \lambda\;$ является корнем квадратного уравнения (2.15). Это уравнение называется характеристическим уравнением для рекуррентного соотношения (2.11).

Для построения базисных решений необходимо различать два случая.

1) Характеристическое уравнение имеет два различных корня $ \;\lambda_1\;$ и $ \;\lambda_2.$

В этом случае имеем два решения $ \;\lambda_1^n\;$ и $ \;\lambda_2^n.\;$ Чтобы убедиться, что они независимы, покажем, что из формулы

$\displaystyle A_n=C_1\,\lambda_1^n+C_2\,\lambda_2^n\eqno{(2.16)}$

путем подходящего выбора констант можно получить любое решение (2.11). Этот факт выражают словами: формула (2.16) -- это общее решение рекуррентного соотношения (2.11).

Для доказательства последнего утверждения рассмотрим произвольное решение  $ \;A_n^\ast.\;$ Выберем константы $ \;C_1^\ast\;$ и $ \;C_2^\ast\;$ так, чтобы $ \;C_1^\ast\,\lambda_1^n+C_2^\ast\,\lambda_2^n\;$ и $ \;A_n^\ast\;$ совпадали при $ \;n=0\;$ и $ \;n=1\;:$

$\displaystyle C_1^\ast\lambda_1^0+C_2^\ast\lambda_2^0=A_0^\ast\;,$

$\displaystyle C_1^\ast\lambda_1+C_2^\ast\lambda_2=A_1^\ast\;. \eqno{(2.17)} $

Условия (2.17) имеют форму линейной системы, определитель этой системы

$\displaystyle \begin{vmatrix} 1 &1\\ \lambda_1 &\lambda_2 \end{vmatrix}=\lambda_2-\lambda_1\ne 0.$

Следовательно, система имеет единственное решение. Из формул (2.17) следует, что два решения $ \;C_1^\ast\,\lambda_1^n+C_2^\ast\,\lambda_2^n\;$ и $ \;A_n^\ast\;$ совпадают в первых двух членах, как мы видели выше, это означает, что они совпадают при всех $ \;n,\;$ то есть

$\displaystyle \;A_n^\ast\;=\;C_1^\ast\,\lambda_1^n+C_2^\ast\,\lambda_2^n\;.$

2) Характеристическое уравнение имеет кратные корни $ \;\lambda_1=\lambda_2.$

В этом случае имеется только одно решение в виде геометрической прогрессии -- $ \;\lambda_1^n,\;$ однако пространство решений двумерно и необходимо построить второе решение. Оказывается, что в рассматриваемом случае решением является последовательность $ \;A_n=n\,\lambda_1^n.\;$

Действительно, так как $ \;\lambda_1\;$ -- кратный корень характеристического уравнения (2.15), то само уравнение имеет вид

$\displaystyle (\lambda -\lambda_1)^2=0\quad\hbox{или}\quad \lambda^2=2\,\lambda_1\,\lambda-\lambda_1^2\;,$

то есть исходное рекуррентное соотношение (2.11) в данном случае имеет следующий вид

$\displaystyle A_n=2\,\lambda_1\,A_{n-1}-\lambda_1^2\,A_{n-2}\;.$

Подставляя в него $ \;A_n=n\,\lambda_1^n,\;$ получаем

$\displaystyle n\,\lambda_1^n=2\,\lambda_1\,(n-1)\,\lambda_1^{n-1}-\lambda_1^2\,(n-2)\,\lambda_1^{n-2}\;.$

После деления на $ \;\lambda_1^n,\;$ получим тождество

$\displaystyle n=2\,(n-1)-(n-2)\;.$

Доказательство того, что решения $ \;\lambda_1^n\;$ и $ \;n\,\lambda_1^n\;$ образуют базис в пространстве решений проводится так же, как в п.1). Формула

$\displaystyle A_n=C_1\,\lambda_1^n+C_2\,n\,\lambda_1^n\;-\eqno{(2.18)}$

общее решение, так как для любого решения $ \;A_n^\ast\;$ можно подобрать $ \;C_1\;$ и $ \;C_2\;$ так чтобы это решение и (2.18) совпадали в первых двух членах. Система для определения констант имеет вид

  $\displaystyle C_1^\ast=A_0^\ast\;$    
  $\displaystyle C_1^\ast\lambda_1+C_2^\ast\lambda_1=A_1^\ast$    

и ее однозначная разрешимость не вызывает сомнения.
Общий случай

В случае соотношения $ \;k$-го порядка (2.10) имеют место утверждения, аналогичные тем, которые были подробно рассмотрены для уравнений 2-го порядка.

1) Совокупность всех решений линейного рекуррентного соотношения $ \;k$-го порядка является подпространством в пространстве всех последовательностей.

2) Размерность этого подпространства равна $ \;k.\;$ (Каждое решение однозначно определяется своими первыми $ \;k\;$ значениями.)

3) Для построения базиса подпространства решений составляется характеристическое уравнение

$\displaystyle \lambda^k=\alpha_1\,\lambda^{k-1}+\alpha_2\,\lambda^{k-2}+\ldots +\alpha_k\;.\eqno{(2.19)}$

(Оно получается, если в рекуррентное соотношение (2.10) подставить $ \;A_n=\lambda^n.\;$) Многочлен

$\displaystyle H(x)=x^k-\alpha_1\,x^{k-1}-\alpha_2\,x^{k-2}-\ldots -\alpha_k\;\eqno{(2.20)}$

будем называть характеристическим многочленом рекуррентного соотношения (2.10).

4) Если характеристическое уравнение имеет $ \;k\;$ различных корней

$\displaystyle \lambda_1\;,\;\lambda_2\;,\;\ldots\;,\;\lambda_k\;,$

то общее решение линейного рекуррентного соотношения (2.10) имеет вид

$\displaystyle C_1\,\lambda_1^n+C_2\,\lambda_2^n+\ldots +C_k\,\lambda_k^n\;.$

При заданных начальных значениях решения $ A_i=a_i,\,i=0,1,\ldots ,k-1,\,$ константы $ \;C_i\;$ можно найти, решая систему

  $\displaystyle C_1\;\lambda_1^0+C_2\;\lambda_2^0+\ldots +C_k\;\lambda_k^0=a_0$    
  $\displaystyle C_1\;\lambda_1+C_2\;\lambda_2+\ldots +C_k\;\lambda_k=a_1$    
  $\displaystyle \quad\ldots\hskip100pt\ldots$    
  $\displaystyle C_1\;\lambda_1^{k-1}+C_2\;\lambda_2^{k-1}+\ldots +C_k\;\lambda_k^{k-1}=a_{k-1}\;.$    

5) Если $ \;\lambda\;$ -- корень характеристическое уравнение кратности $ \;e,\;$ то рекуррентное соотношение (2.10) имеет следующие решения

$\displaystyle \lambda^n\;,\;n\,\lambda^n\;,\;\ldots\;,\;n^{e-1}\lambda^n\;.$

(Очередное решение получается из предыдущего умножением на $ \;n.\;$)

Пусть характеристическое уравнение (2.19) имеет корни

  $\displaystyle \lambda_1\quad\hbox{кратности}\;\;e_1\;,$    
  $\displaystyle \lambda_2\quad\hbox{кратности}\;\;e_2\;,$    
  $\displaystyle \ldots\ldots$    
  $\displaystyle \lambda_r\quad\hbox{кратности}\;\;e_r\;,$    
  $\displaystyle e_1+e_2+\ldots +e_r=k$    

(Таким образом,

$\displaystyle H(x)=(x-\lambda_1)^{e_1}(x-\lambda_2)^{e_2}\ldots (x-\lambda_r)^{e_r}\;).$

Тогда общее решение линейного рекуррентного соотношения (2.10) имеет вид

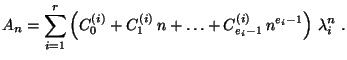
$\displaystyle A_n =\sum_{i=1}^r\left(C_0^{(i)}+C_1^{(i)}\,n+\ldots + C_{e_i-1}^{(i)}\,n^{e_i-1}\right)\,\lambda_i^n\;.$

Продолжение примера 1. Для рекуррентного соотношения

$\displaystyle A_n=A_{n-1}+A_{n-2}\;,$

которому удовлетворяет число двоичных слов, в которых не встречается подряд двух единиц, имеет вид

$\displaystyle \lambda^2=\lambda+1\;.$

Найдя его корни $ \;\lambda_1=\frac {1+\sqrt{5}}2\;$ и $ \;\lambda_2=\frac {1-\sqrt{5}}2,\;$ получим общее решение

$\displaystyle A_n=C_1\,\lambda_1^n+C_2\,\lambda_2^n\;.$

Для определения констант, учитывая, что $ \;A_1=2,\,A_2=3,\,$ составляем систему

$\displaystyle \begin{displaymath}\eqalign{$ $\displaystyle C_1\lambda_1+C_2\lambda_2=2$    
  $\displaystyle C_1\lambda_1^2+C_2\lambda_2^2=3\;.$    

Решая ее, найдем C_1=&lambda#lambda;_1^2&lambda#lambda;_1-&lambda#lambda;_2,    C_2=-&lambda#lambda;_2^2&lambda#lambda;_1-&lambda#lambda;_2.Отсюда $ \;A_n=\frac {\lambda_1^{n+2}-\lambda_2^{n+2}}{\lambda_1-\lambda_2}\;$ или

$\displaystyle A_n=\frac 1{\sqrt{5}}\left (\left(\frac {1+\sqrt{5}}2\right )^{n+2}-\left (\frac {1-\sqrt{5}}2\right )^{n+2}\right)\;.\eqno{(2.21)}$

Выше говорилось о преимуществе явной формулы, подтвердим это на примере $ \;A_n.\;$ Допустим, что длинную последовательность 0 и 1 (например, бинарный файл) нужно передать по каналу связи. Канал имеет два состояния: одно для передачи 0 и одно для передачи 1, однако, из-за технических ограничений состояния, в которых передаются 1, не могут следовать друг за другом. В этих условиях исходная последовательность 0 и 1 предварительно кодируется: последовательность разбивается на блоки длины $ \;m\;$ и каждый блок заменяется правильным словом длины $ \;n.$

Практический интерес представляет такой вопрос. Во сколько раз увеличивается длина блока в результате его кодирования -- в это же количество раз увеличивается время пересылки последовательности по рассматриваемому каналу по сравнению с двоичным каналом без ограничений на чередование состояний.

Для того чтобы правильных слов длины $ \;n\;$ хватило для кодирования $ \;2^m\;$ возможных блоков длины $ \;m,\;$ число $ \;n\;$ надо выбирать под условием $ \;A_n\ge 2^m\;$ или после логарифмирования

$\displaystyle \;{\rm log}_2\,A_n\ge m\;.\eqno{(2.22)}$

Найдем как ведет себя $ \;{\rm log}_2\,A_n,\;$ при $ \;n\to\infty.\;$ В формуле (2.21) $ \;\lambda_1=\frac {1+\sqrt{5}}2\approx 1,618,\;\lambda_2=\frac {1-\sqrt{5}}2\approx -0,618,\;$ следовательно, $ \;\left(\frac {\lambda_2}{\lambda_1}\right)^n\to 0\;$ при $ \;n\to\infty\;.$ Используя этот факт легко находим, что $ \;\lim\limits_{n\to\infty}\frac {{\rm log}_2\,A_n}n={\rm log}_2\lambda_1\approx 0,694\;.$ Следовательно, $ \;{\rm log}_2\,A_n\approx 0,694\,n\;$ и условие (2.22) принимает вид

$\displaystyle 0,694\,n\ge m\quad\hbox{или}\quad n\ge \frac 1{0,694}\,m=1,44\,m\;.$

Таким образом, после кодирования длина последовательности увеличивается примерно в полтора раза.

Hosted by uCoz