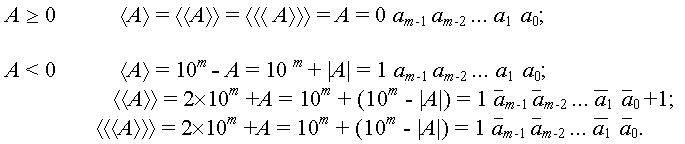
25.
Десятичная арифметика ЭВМ (лекция 25)Следует различать два уровня понятий, используемых при описании десятичной машинной арифметики: уровень десятичный, касающийся всего числа, и уровень двоичный, на котором раскрываются действия над тетрадами.
На десятичном уровне можно определить коды: прямой, дополнительный и обратный. Считая числа целыми со знаком в старшем бите и обозначая число десятичных цифр в принятом
n -- разрядном формате через m = (n -- 1)/4, получим: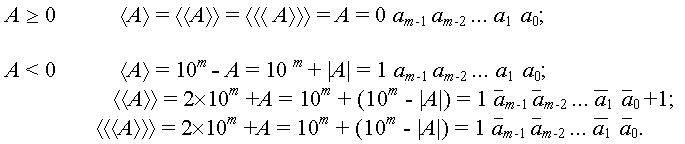
Здесь, как и прежде, одинарные угловые скобки означают прямой код, двойные – дополнительный и тройные – обратный. Черта означает десятичное дополнение до 9. Знаковая цифра остается двоичной, даже если это модифицированный код. При арифметическом сдвиге вправо дополнительного и обратного кода отрицательного числа освободившийся десятичный разряд занимается девяткой. Своеобразно выполняется модифицированный сдвиг вправо после переполнения. Вместо цифры 0 формируется тетрада, изображающая цифру 8. Это объясняется тем, что нуль в двоичной системе дополняет единицу до единицы, а в десятичной системе требуется получить дополнение единицы до девяти. При арифметическом сдвиге влево дополнительного кода освободившаяся тетрада занимается нулем, а при сдвиге обратного кода - девяткой. Примеры арифметических сдвигов:
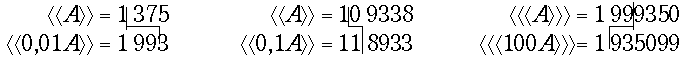
Кроме отмеченных особенностей представления отрицательных чисел, на десятичном уровне раскрываются детали вычислений, связанные с большим числом допустимых цифр. При умножении и делении получение каждого частичного произведения или очередного остатка перестает быть элементарным одношаговым действием и превращается в несколько последовательных элементарных операций.
На двоичном уровне, как уже говорилось, раскрываются операции над тетрадами, заменяющими десятичные цифры. Представление десятичных чисел в зонном и упакованном форматах было описано в одной из первых лекций данного раздела курса, а здесь мы рассмотрим особенности выполнения арифметических операций.
Недостатком кода 8421 является сложность инвертирования тетрад, т.е. получения арифметического дополнения до 9. Разумеется, преобразование
![]()
Обращение тетрады сводится к инвертированию всех цифр тетрады и прибавлении константы "десять" (1010) по модулю 16, так как возникающий из тетрады перенос игнорируется.
Если нужно преобразовать прямой код многоразрядного числа в дополнительный, или наоборот, кроме прибавления 10 по модулю 16 ко всем тетрадам, к младшей тетраде нужно прибавить единицу и выполнить возникающие при этом переносы. Это, казалось бы, простое требование нуждается в уточнении. Рассмотрим обращение кода, оканчивающегося нулями:

Переносы, возникающие между тетрадами при сложении с поправочной константой, показаны в рамках. Они игнорируются в соответствии с установленным правилом. Но перенос, который должен был бы возникнуть после сложения с единицей младшего разряда, здесь не получается, вместо этого появляется неправильная тетрада 1010.
Правильный результат получается только в том случае, если единица младшего разряда прибавляется сразу после инвертирования, а возникающие при этом переносы передаются из тетрады в тетраду. Только после этого должно происходить прибавление константы 1010 и лишь к тем тетрадам, из которых не было переноса:
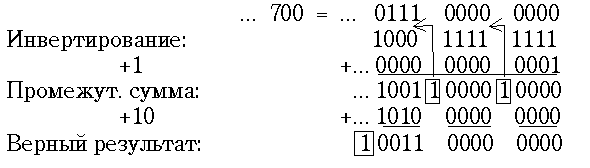
Для правильного обращения тетрад кода 8421 в арифметическом блоке необходимо иметь для каждой тетрады отдельный триггер переноса
AF (так называемый "флаг полупереноса" или флаг "вспомогательного переноса" ). После сложения с константой 10 состояние этого триггера игнорируется, а при обычном сложении оно передается в старшую тетраду. Микрооперация прибавления константы +10 избирательно в те тетрады, из которых при сложении не было переноса, называется "десятичной коррекцией суммы" или просто "десятичной коррекцией".При сложении тетрад кода 8421 нужно получить верную цифру суммы в данном десятичном разряде и выделить единицу десятичного переноса. Чтобы превратить десятичное переполнение тетрады в шестнадцатеричное и вызвать появление межтетрадного переноса, можно применить поправку +6.
Рассмотрим возможные ситуации: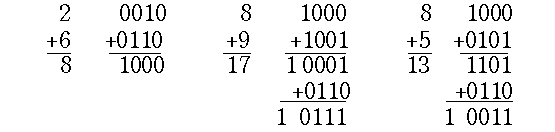
В первой ситуации поправка не нужна. Во второй - шестнадцатеричное переполнение уносит лишнюю шестерку, и её потерю можно скомпенсировать поправкой +6. В третьей ситуации шестнадцатеричный перенос сам не возникает, но его можно вызвать сложением с поправкой +6. Следовательно, управление поправкой требует анализа состояний триггеров полупереноса (вторая ситуация) и выявления неправильных тетрад (третья ситуация).
При этом методе параллельное сложение многоразрядных чисел не может быть завершено за две микрооперации (сложения и коррекции) и превращается в многошаговый процесс. Возьмем такой пример:

Видно, что число шагов сложения зависит от случайного сочетания цифр слагаемых, а максимальное число шагов коррекции равно числу десятичных разрядов.
Чтобы избежать этого, в машине с параллельной десятичной арифметикой, должен применяться усовершенствованный способ коррекции. Ко всем тетрадам одного из слагаемых "авансом" прибавляется излишек +6. У правильных тетрад перенос при этом не возникает, что, между прочим, позволяет обнаруживать неправильные тетрады во входных данных. Затем делается сложение, а после него - одношаговая коррекция прибавлением 10 в те тетрады, откуда не было переноса при сложении чисел. Таким образом, удается не только устранить повторные поправки, но и использовать ту же самую микрооперацию коррекции, что и при обращении кодов: поправку +10. Выполним по этому способу сложение чисел из предыдущего примера:
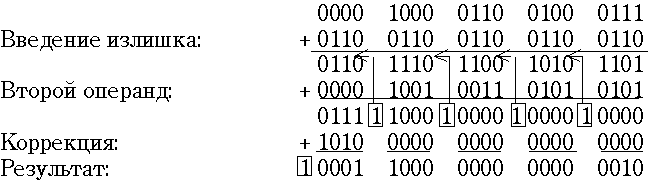
Рассмотрим операции над числами в символьной форме. Эти операции характерны для ПЭВМ. Они выполняются по загружаемой программе и требуют минимальных аппаратных средств. Числа обрабатываются последовательно, цифра за цифрой, причем каждая из них представлена байтом зонного формата в коде
ASCII (American standard code for information interchange). В старшей (зонной) половине байта находится тетрада 0011, а в младшей - цифровая тетрада кода 8421. Числа обрабатываются, начиная с младших разрядов, код знака поступает первым. В операциях участвует только один байт сумматора и аккумулятора; переносы контролируются основным и вспомогательными триггерами CF и AF. Кроме того, тетрады контролируются логическими схемами, выявляющими неправильные тетрады (см. рис. 25.1). Перед выполнением над очередным байтом арифметической операции его зонная тетрада обнуляется сложением байта с константой 1101 0000 и перед выгрузкой байта восстанавливается сложением с константой 0011 0000.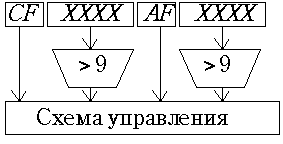
Рис. 25.1
Сложение выполняется программой с циклическим повторением однотипных шагов. В первом цикле сбрасывается
CF := 0. Затем в младшей тетраде аккумулятора образуется сумма двух очередных цифр слагаемых (операция ADC). Если сумма превышает 15, то происходит перенос, фиксируемый флагом AF. Если получается неправильная тетрада, то она обнаруживается логической схемой. После этого к младшей тетраде прибавляется поправка + 6 (операция ААА). Это происходит при AF = 1 или при неправильной тетраде. Возникающий в последнем случае перенос устанавливает триггер AF. Происходит установка CF:=AF. Полученный байт результата выгружается, после чего начинается следующий цикл. Все операции, как уже говорилось, выполняются программным путем, причем для операции сложения используется та же команда ADC, что и для сложения двоичных беззнаковых чисел, а для десятичной коррекции результата - команда ААА.Вычитание тоже начинается так, как будто числа не десятичные, а двоичные, беззнаковые. В первом цикле устанавливается
CF:=1. По команде SBB тетрада второго операнда инвертируется и прибавляется к тетраде первого операнда с учетом значения CF. Например: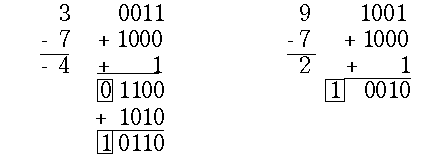
В первом примере поправка +10 по модулю 16, т.е. вычитание 6 делается, чтобы устранить излишек 6, получившийся при инвертировании тетрады 7. О необходимости коррекции говорит
AF = 0. Кроме того, по AF=0 происходит установка CF:=0, что означает необходимость заема из старшего разряда (заем реализуется, как отсутствие единицы переноса). Перенос в AF, возникающий после коррекции, игнорируется. Во втором примере результат сразу получается верным. Поскольку AF = 1, коррекция не требуется. Триггер CF устанавливается в единичное состояние, что означает отсутствие заема из старшей тетрады.Пример вычитания многоразрядных чисел:
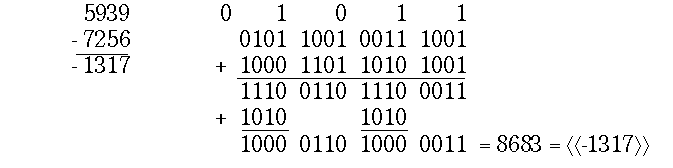
В первой строке примера показаны последовательные (справа налево) состояния триггера полупереноса
AF . Такие же состояния проходит триггер переноса из байта в байт CF. Нулевое состояние триггеров соответствует передаче единицы заема, единичное – отсутствию заема. Во второй строке записаны прямые значения тетрад уменьшаемого, а в третьей – инверсии тетрад вычитаемого. В четвертой строке записана промежуточная сумма, требующая коррекции в зависимости от состояния триггера полупереноса. Результат операции, если он отрицательный, представляется в дополнительном коде.Умножение требует ещё более сложной организации последовательного процесса, в котором кроме основного цикла получения очередного частичного произведения и его сложения с накапливаемой суммой, существует еще и внутренний цикл умножения очередной цифры множимого.
Процесс организуется загружаемой программой, включающей операции обнуления зонных тетрад и их последующего восстановления, двоичного умножения очередных байтов, содержащих числовые данные только в младшей тетраде, коррекцию произведения по команде ААМ и его сложения с суммой частичных произведений (с коррекцией по команде ААА
).Рассмотрим процесс коррекции умножения на примере. Допустим, что в данном цикле умножаются цифры 9
*9 = 81. В результате умножения байта множимого на байт множителя (с обнуленными зонными тетрадами), в аккумуляторе находится двоичное число 81 (верхняя строка примера):
Число сложений с константой + 6 определяется первоначальным содержанием старшей тетрады байта произведения, плюс числом переносов, возникающих в ходе коррекции, плюс единица, если в конце получается неправильная тетрада. Перенос, возникающий в конце операции после исправления неправильной тетрады уже не вызывает нового шага коррекции.
При составлении программ умножения на языке ассемблера используются двоичные команды
MUL и ADD (ADC) с коррекцией умножения ААМ и сложения ААА, а также константы для управления зонными тетрадами. Аналогично программируется деление с использованием команд двоичной арифметики DIV и SUB (SBB) c командами коррекции AAD и AAS. Обработка десятичных чисел в упакованных форматах в ПЭВМ очень ограничена. Возможны только две операции: сложение и вычитание байтов, содержащих по две десятичные цифры. При этом используются другие, "двухразрядные" поправки: DAA при сложении и DAS при вычитании. B зависимости от состояния триггеров CF и AF и наличия неправильных тетрад прибавляются или вычитаются байты 06, 60 или 66. В специализированных машинах десятичные числа могут быть представлены только в упакованном формате. Преимущественно в упакованном формате они обрабатываются и в крупных универсальных машинах, а зонный формат применяется в них только при вводе и выводе.Алгоритмы обработки упакованных многоразрядных чисел удобно описывать, сравнивая их с двоичными алгоритмами, так как отличия обуславливаются в первую очередь именно переходом к другой системе счисления, а что касается последовательной или параллельной обработки, то возможен любой из этих вариантов. На практике используют комбинированный способ, когда десятичные числа переменной длины обрабатываются частями по одному или два байта.
Предположим для простоты, что десятичные данные имеют постоянную длину
n = 4m +1 двоичных разрядов, что знаковая цифра занимает старший разряд, и что применяется параллельная обработка. Операнды загружаются в процессор в прямом коде и в таком же коде должны быть представлены перед выгрузкой.Сложение
А := В +С может быть выполнено по микропрограмме, напоминающей сложение двоичных мантисс в прямом коде. Как и в случае мантисс, числа, а точнее - одно из чисел, переводится в дополнительный код только в случае несовпадения их знаков. Отрицательная сумма сперва получается в дополнительном коде и переводится в прямой код перед выгрузкой. Сумматор и регистр-аккумулятор не имеют разряда для знаковой цифры. Знак результата определяется по состоянию флага CF.Главное отличие десятичной микропрограммы состоит в необходимости десятичной коррекции суммы. На рис. 25.2 показана микропрограмма сложения по методу с предварительным внесением излишков + 6 в каждую тетраду одного из слагаемых. Триггер
CF используется для контроля переполнения (при совпадении знаков слагаемых) или для определения знака суммы (при разных знаках слагаемых).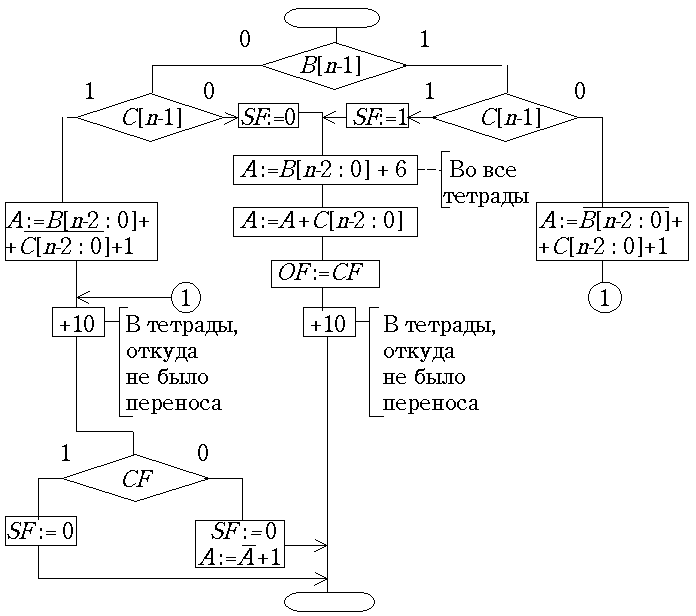
Рис. 25.2
Умножение десятичных чисел усложнено по сравнению с двоичным умножением, невозможностью заменять сдвигами умножение на цифры 3, 5, 6, 7 и 9. Поэтому приходится, например, при умножении на 7 семикратно выполнять операцию А
:= А +В[n-2 : 0], каждый раз сопровождая её десятичной коррекцией.С некоторыми упрощениями процесс можно представить следующим образом. Сперва к каждой тетраде множимого
B прибавляется константа "+6"; сумма оказывается в аккумуляторе. Подготовленное множимое возвращается в регистр В, а аккумулятор обнуляется. В счетчик основных циклов CTR 1 записывается число десятичных цифр множителя m =(n-1)/4.В начале каждого из основных циклов в счетчик числа сложений
CTR 2 заносится младшая тетрада множителя С[3:0]. Содержимое счетчика анализируется и, если оно не равно нулю, к сумме частичных произведений А прибавляется содержимое регистра В (разумеется, без знаковой цифры). После сложения происходит десятичная коррекция прибавлением 10 по модулю 16 к тетрадам, из которых не было переноса. Малый цикл заканчивается вычитанием единицы из CTR 2. Если после этого счетчик CTR 2 не обнулился, сложение повторяется.При обнулении счетчика
CTR 2 основной цикл, соответствующий одной цифре множителя, заканчивается. Сумма частичных произведений А и множитель С сдвигаются на одну тетраду вправо, из CTR 1 вычитается единица и начинается следующий основной цикл.Если операнды - целые числа, то, как и при умножении двоичных чисел, разрядная сетка произведения должна удваиваться по сравнению с сетками сомножителей. Практически это означает необходимость использования аккумулятора в виде регистровой пары АН и
AL, причем с сумматором непосредственно связан только регистр АН.Характерной особенностью десятичного умножения является то, что для временного хранения переполнения в промежуточных стадиях процесса нельзя обойтись триггером переноса
CF, как в двоичной арифметике. Значение переполнения может доходить до девяти. Поэтому аккумулятор должен иметь слева не один разряд для хранения переполнения, а дополнительную тетраду, и такую же тетраду должен иметь сумматор для передачи переносов.Знак произведения, как это вообще делается при умножении прямых кодов, определяется логически. При подготовке произведения к выгрузке в формате числа двойной длины по состоянию триггера
SF должен быть сформирован знаковый бит (или знаковая тетрада). Схема микропрограммы умножения показана на рис. 25.3.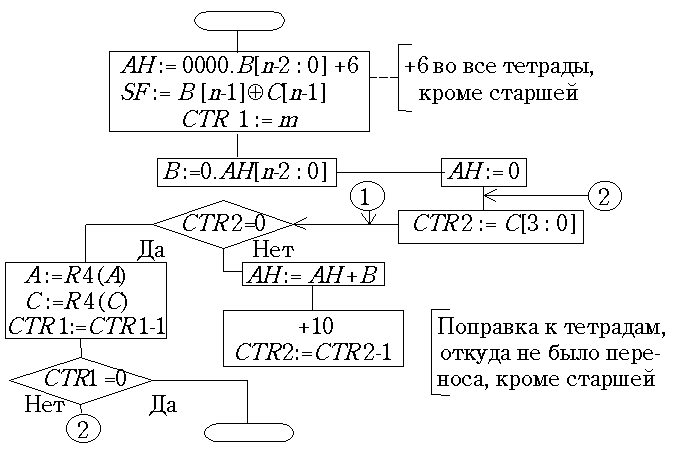
Рис. 25.3
Старшая тетрада аккумулятора А в этой микропрограмме используется только для временного хранения нескольких переносов из основной части разрядной сетки. Сложения в той тетраде не происходят, поэтому не требуется и её коррекция. Необходимо заметить, что практические микропрограммы десятичного умножения при параллельно-последовательной обработке чисел содержат еще и третий, внутренний цикл, в котором по частям выполняется очередной сложение из описанного здесь малого цикла по счетчику
CTR 2.Деление представляет самую сложную из арифметических операций, выполняемых аппаратно. Допустим, что перед началом операции делимое находится в регистре А, делитель - в регистре В. Частное формируется в регистре
D. Делимое имеет двойную длину, причем младшая его половина может первоначально размещаться в регистре D. Эту возможность в микропрограмме мы использовать не будем, концентрируя внимание на главных деталях процесса.На рис. 25.4 показан состав оборудования для деления упакованных чисел. Два вспомогательных регистра С и
G в начале операции свободны. Один из них нужен для хранения модуля делителя с минусом в дополнительном коде, а второй - для организации пересылок.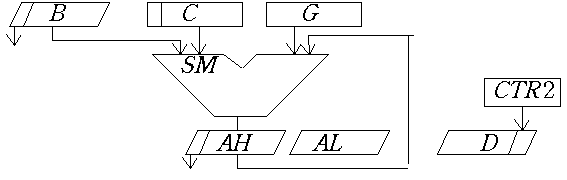
Рис. 25.4
В основе операции лежит алгоритм с восстановлением остатка, так как в десятичной арифметике правила деления без восстановления остатка получаются слишком сложными. Сдвигами управляет счетчик
CTR 1, который на рисунке не показан. В каждом из основных циклов, контролируемых этим счетчиком, выполняется несколько вычитаний, вплоть до получения отрицательного остатка. Количество вычитаний подсчитывается счетчиком CTR 2.Схема микропрограммы приведена на рис. 25.5. Предполагается, что
A № 0 и В № 0, иначе пришлось бы в начале микропрограммы вводить соответствующие проверки. Перед началом основных операций выполняется выравнивание делимого и делителя по левому краю. Для этого проверяется равенство нулю старших тетрад делимого и делителя. При этом возможны четыре ситуации. Когда обе тетрады равны нулю, оба числа сдвигаются влево, частное не меняется, декремент счетчика CTR 1 не делается. Когда равна нулю только тетрада делимого, выполняются сдвиги и декремент счетчика. В этой ситуации сдвиг регистра D заменяет предварительное обнуление этого регистра. Когда равна нулю только тетрада делителя, устанавливается флаг переполнения и микропрограмма прерывается. В четвертой ситуации, когда ни одна из проверяемых тетрад не равна нулю, начинается подготовка к основной части микропрограммы. Старшая часть делимого из регистра AH временно пересылается во вспомогательный регистр G, а в AH формируется обратный код делителя с излишком “6” в каждой тетраде. Этот код затем пересылается в регистр C . После этого в старшей части регистра-аккумулятора готовится прямой код делителя с излишком и возвращается в регистр делителя. Только после этого старшая половина делимого возвращается в аккумулятор и начинается основной процесс деления (циклы сложений или вычитаний со сдвигом).
Рис. 25.5
При получении отрицательного остатка он восстанавливается, а содержимое счетчика
CTR 2, представляющее очередную цифру частного, переписывается в младшую тетраду регистра D. После этого циклы повторяются до обнуления основного счетчика CTR 1. Несмотря на кажущуюся подробность описанной схемы алгоритма деления, она не полна. Так в ней не приводятся микрооперации формирования знаков остатка и частного, не указывается, каким образом должно происходить расширение числа в аккумуляторе при делении, чтобы операции умножения и деления были аппаратно совместимы и пр.Преобразование десятичных чисел в двоичную систему может выполняться двумя способами. Первый из них основан на формуле
В
= (...((dm-1(2+8)+dm-2)(2+8)+...+d1(2+8)+d0,где В
= bn-1bn-2 ...b1b0 и D = dm-1dm-2...d1d0 - обозначения двоичных (от binary) и десятичных (decimal) модулей чисел. Мы будем здесь обсуждать только преобразование модулей чисел. Преобразование выполняется за m циклов. Десятичное число находится в сдвиговом регистре D, а двоичное накапливается в аккумуляторе, который в данном случае мы обозначим В. В каждом цикле к тетраде В[3:0] прибавляется очередная тетрада числа D, начиная со старшей. Вместо умножения на 10 выполняется сложение +2В + 8В. Для этого содержимое аккумулятора В сдвигается на один разряд влево и копируется в отдельный сдвиговый регистр С. Затем выполняется сложение В с числом С, сдвинутым влево на два разряда. За это время в регистре D выполняется сдвиг влево на одну тетраду. Пример: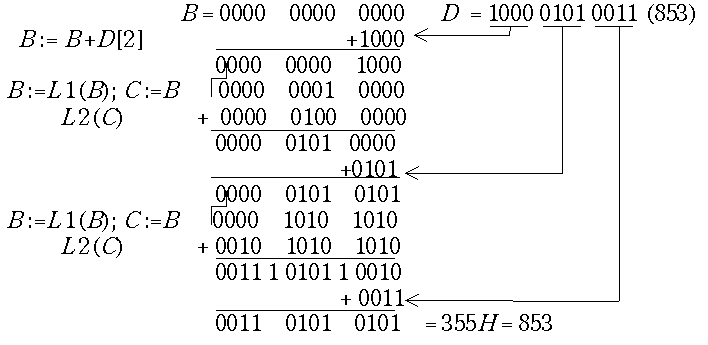
Второй алгоритм преобразования десятичных чисел в двоичные основан на делении десятичного числа на два с запоминанием очередных остатков. Деление заменяется сдвигом числа
D вправо на один двоичный разряд с десятичной коррекцией тех тетрад, куда при сдвиге поступила единица из старшей тетрады. Роль остатков деления исполняют цифры младшего бита D[0], выдвигаемые из разрядной сетки. Они передаются вв старший разряд B[n-1] модуля формируемого двоичного числа.Определим правила коррекции тетрад числа D. Сдвиг тетрады вправо с переходом в неё единицы из старшей тетрады дает результат, равный ]
d[/2 + 8, где ]d[- прежнее значение тетрады, округленное до меньшего четного числа. По правилам десятичной арифметики деление тетрады с единицей переноса на два должно давать]d[/2 + 5.
Стало быть, десятичная коррекция в этом случае должна состоять в вычитании константы "три", что заменяется прибавлением 13 по модулю 16. Итак, коррекция состоит в прибавлении к каждой тетраде, получившей при сдвиге единицу, константы 13 с игнорированием межтетрадного переноса. Пример:
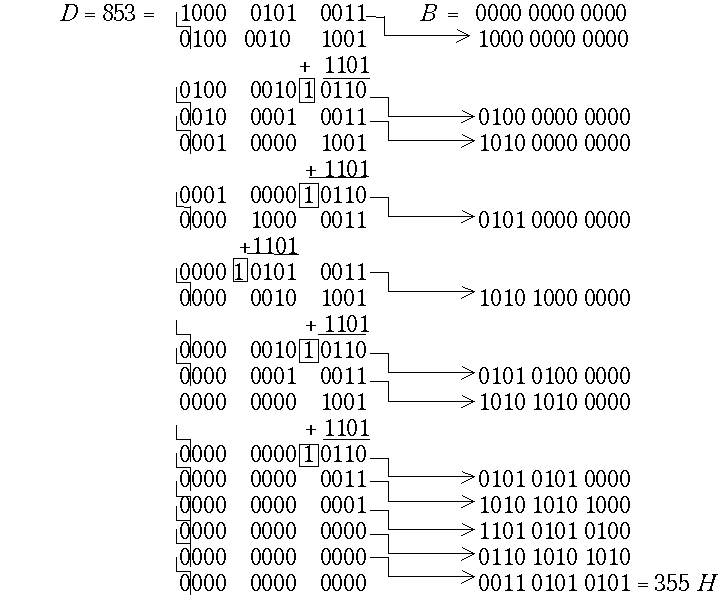
Всего должно быть сделано
n = 4m сдвигов, после чего происходит формирование знакового бита числа.Преобразование из двоичной системы в десятичную может быть выполнено только по одному алгоритму - с умножением на два, так как деление на десять слишком сложно. В основе преобразования лежит формула
|D| = (...((bn-1![]() 2)+bn-2)
2)+bn-2)![]() 2+...+b1)+b0.
2+...+b1)+b0.
Десятичное число формируется в аккумуляторе, который теперь будем обозначать
D. В регистрах В и D в каждом цикле выполняются двоичные сдвиги на один разряд влево. В аккумуляторе это заменяет умножение на два. В освобождающийся младший бит D[0] передается старшая цифра модуля B [n- 2], что заменяет сложение с очередной цифрой В. Кроме того, в каждом цикле производится десятичная коррекция тетрад числа D.Коррекции требуют тетрады, переполняющиеся в результате сдвига. После сдвига в такие тетрады требуется прибавлять поправку “+6”. Можно делать поправку перед сдвигом, и тогда она должна иметь величину не +6, а +3. Признаком необходимости такой заблаговременной коррекции является величина тетрады равная или большая пяти. Пример:
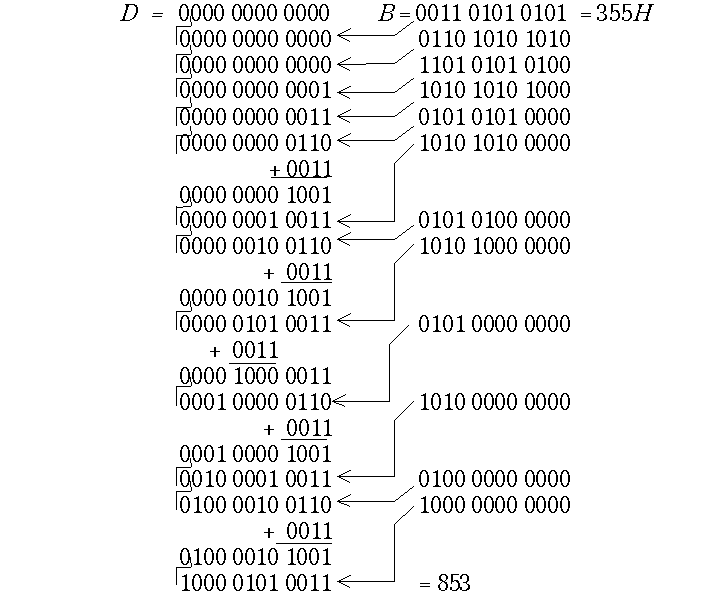
По окончании циклов преобразования системы счисления формируется знаковая цифра (или знаковая тетрада) числа
D.