23

23. Операции с плавающей точкой (лекция 23)

условный формат чисел и состав оборудования,
выравнивание порядков при сложении,
сложение и нормализация мантисс,
схема микропрограммы сложения,
действия над характеристиками при умножении чисел,
умножение мантисс,
деление чисел.

Чтобы нам в дальнейшем, при описании арифметических операций использовать примеры, нужно взять некоторый определенный формат числа с плавающей точкой. Ранее был описан формат КВ (короткое вещественное) длиной 32 разряда, в котором старшая цифра модуля мантиссы явным образом не представлена, поскольку в нормализованной мантиссе она всегда равна единице. Такой формат годится для хранения числа или его пересылки, но для выполнения арифметических операций старшая цифра модуля мантиссы должна быть представлена явно. Включив в формат КВ старшую цифру модуля мантиссы получим условный 33-х разрядный формат из одной знаковой цифры, восьми цифр характеристики, имеющей смещение d_кв =127, и 24 цифр модуля мантиссы, нормализованной по условию 2>|M|1.

Разумеется, мантиссы должны загружаться и выгружаться в прямом коде. Они переводятся в дополнительный код только для сложения чисел с разными знаками или для вычитания чисел с одинаковыми знаками. В соответствии с рассмотренными ранее алгоритмами сложения прямых кодов, сумматор может иметь разрядность модуля мантиссы, а контроль переполнения или выявление знака результата может осуществляться с помощью триггера переноса. Здесь мы будем для триггеров переноса, как и для других логических признаков, использовать (в значительной степени условно) обозначения, принятые в ассемблере для операций с плавающей точкой.

Допустим, что в процессоре имеется два отдельных сумматора: восьмиразрядный - для характеристик и 24-х разрядный - для мантисс. Это упростит микропрограммы по сравнению с вариантом, когда используется только один 24-х разрядный сумматор. Не будет лишних пересылок чисел из регистра в регистр, операций очистки регистров и расширения чисел. Состав оборудования для сложения чисел с плавающей точкой с учетом всех сделанных оговорок показан на рис. 23.1.

Рис. 23.1

Сложение чисел с плавающей точкой состоит из трех последовательно выполняемых операций: выравнивание порядков, сложение мантисс и нормализация результата.

Выравнивание порядков начинается с вычитания из характеристики первого операнда характеристики второго. Для этого характеристика второго операнда инвертируется, то есть вычитание происходит так же, как с дополнительными кодами.

Например:

E_B = 16; E_B + d = 16+127 = 143 = 1000 1111;

E_C = 12; E_C + d = 12+127 = 139 = 1000 1011;

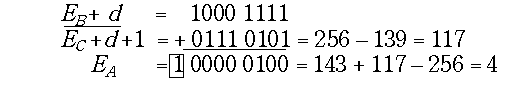
Исследование этого примера показывает, что характеристики можно вычитать как дополнительные коды, хотя они являются другой смещенной системой представления чисел и не имеют знаковой цифры. При вычитании получается истинная разность порядков чисел, а не новая характеристика. В данном случае получилась положительная разность, но аналогично получается и отрицательный результат:

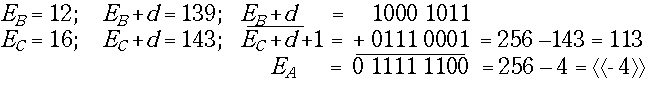
Видно, что и в этом случае получается разность порядков, а не характеристика, причем отрицательная разность представлена в дополнительном коде. Перенос из старшего разряда характеристики во втором примере не получился, и мы можем заключить, что наличие или отсутствие этого переноса следует использовать как признак знака полученной разности: перенос получается при положительной разности, т.е. когда большую характеристику имеет первый операнд..

Если большей оказалась характеристика первого операнда, то необходимо разнормализовать второй операнд таким образом, чтобы порядки операндов выровнялись. Для этого модуль второй мантиссы пересылается в сдвиговый регистр D (или аккумулятор, если он выполнен как сдвиговый регистр) и там сдвигается вправо на величину разности порядков. Характеристика второго операнда не изменяется, так как в дальнейших действиях она не участвует и, в конце концов, игнорируется. Характеристика первого операнда непременно сохраняется и временно (до нормализации) представляет характеристику результата. Если большей оказалась вторая характеристика, то разнормализуется первый операнд, а его характеристика замещается характеристикой второго операнда.

Сложение мантисс происходит, в общем, так же, как сложение целых чисел в прямом коде. При совпадении знаков операндов триггер переноса CE 2 контролирует переполнение мантисс, а при противоположных знаках слагаемых он выявляет знак результата: он содержит единицу при положительной сумме. Разумеется, при сложении чисел с разными знаками отрицательный операнд переводится в дополнительный код. Схема микропрограммы сложения с плавающей точкой показана на рис. 23.2.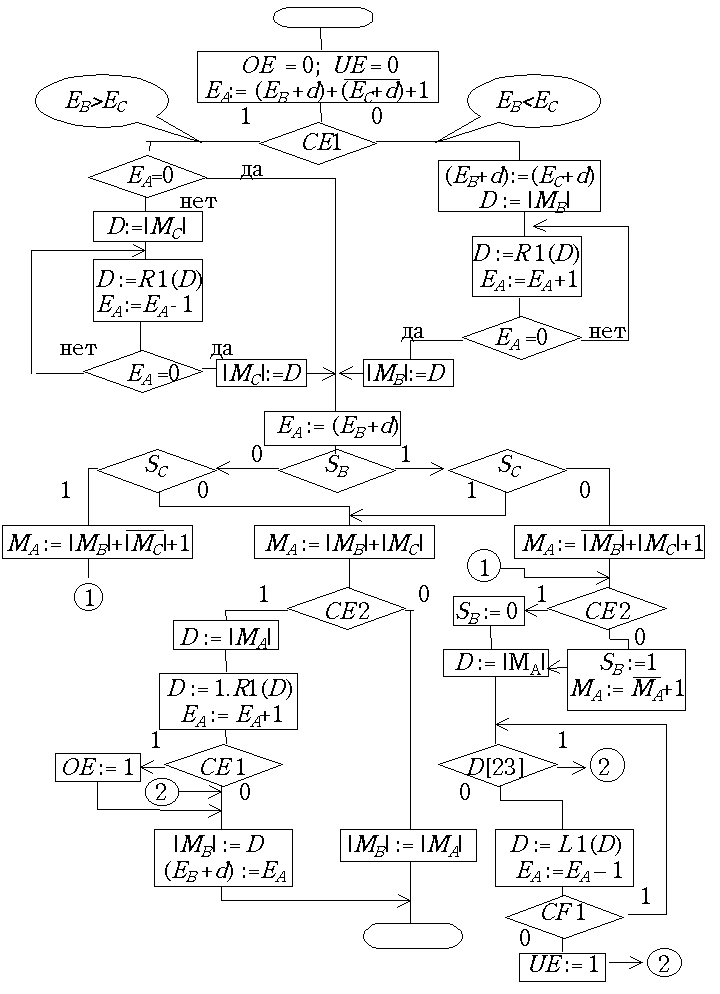

Рис. 23.2

Нормализация результата может понадобиться в двух случаях. Если при сложении мантисс произошло переполнение, то требуется нормализация вправо. Модуль мантиссы сдвигается вправо, в освободившийся разряд записывается единица. Одновременно к характеристике прибавляется единица и анализируется состояние триггера CE 1. Единица в этом триггере означает переполнение характеристики.

Во втором случае, когда в одном или нескольких старших разрядах модуля мантиссы находятся нули, требуется нормализация влево. Процесс нормализации при этом происходит циклически: сдвиги мантиссы влево и вычитания единицы из характеристики повторяются до тех пор, пока в старшем разряде модуля не окажется единица.

При умножении чисел с плавающей точкой характеристики сомножителей В и С складываются. Из полученной суммы формируется характеристика произведения. Сложение характеристик само по себе дает сумму истинных порядков, уменьшенную на два. Дело в том, что происходит перенос, уносящий единицу с весом 256, что на два больше удвоенного смещения. Чтобы исправить сумму до верного изображения характеристики, нужно прибавить константу d + 2 = 129. Например: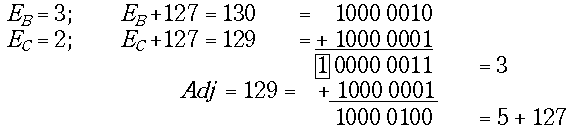

Перенос из старшего разряда характеристики может произойти не сразу, на первом шаге, а на втором, т.е. во время коррекции:

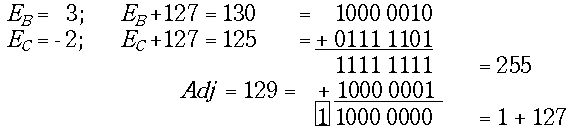
При сложении характеристик может произойти переполнение или антипереполнение характеристик. В первом случае перенос в CE 1 получается двукратным, а во втором - вообще не происходит. Примеры: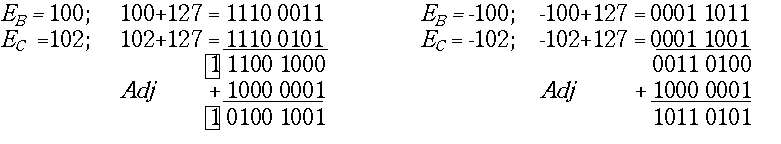

Перемножение мантисс происходит так же, как и целых чисел в прямом коде. Число циклов равно числу цифр множителя, т.е. равно числу разрядов модуля стандартной мантиссы. Последний цикл, как при умножении целых чисел, делается без сдвига. При принятом условии нормализации максимальное значение мантиссы произведения меньше четырех:

Поэтому переполнение мантиссы ограничивается только одним разрядом, единица переполнения сохраняется в триггере переноса CE 2. Такое переполнение исправляется нормализацией вправо, но при этом может случиться переполнение характеристики. Схема микропрограммы умножения с показана на рис. 23.3.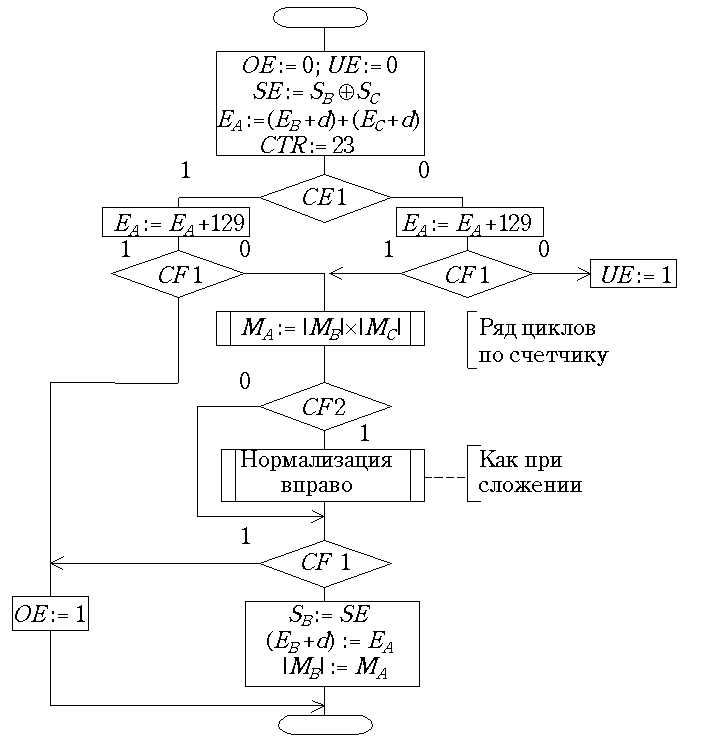

Рис. 23.3

При делении чисел с плавающей точкой процесс организован аналогично, но характеристики не складываются, а вычитаются, поправочная константа равна не 129, а 127. Мантиссы делятся как числа в прямом коде. При получении в одном из промежуточных циклов нулевого остатка сложения - вычитания прекращаются, и над частным производится нужное число сдвигов. Остаток в любом случае не сохраняется. По окончании деления может понадобиться нормализация влево с контролем антипереполнения. Упрощенная схема микропрограммы деления показана на рис. 23.4.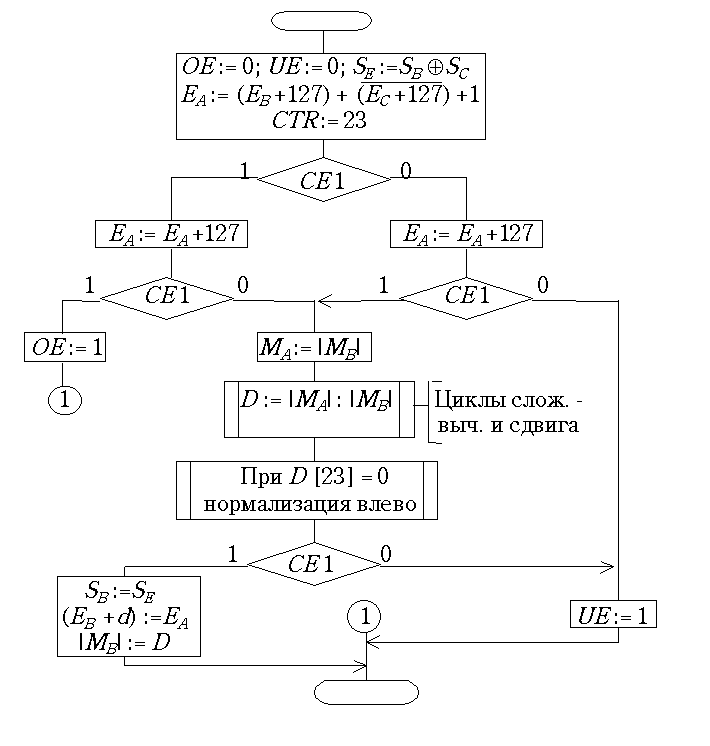

Рис. 23.4

Содержание