21.
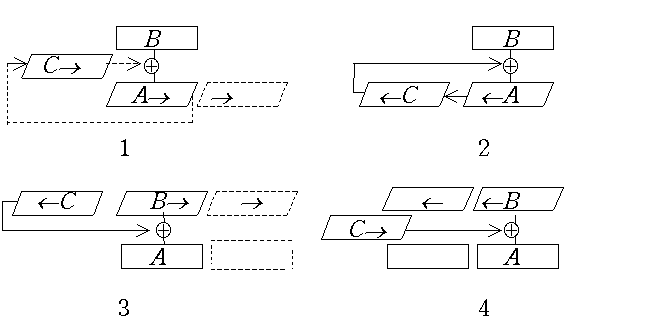
Варианты умножения прямого кода. Ускоренное умножение с группировкой разрядов (лекция 21)В предыдущей лекции был рассмотрен вариант алгоритма умножения прямых кодов, в котором множитель и сумма частичных произведений в каждом цикле сдвигались на один разряд вправо. Всего же существует четыре варианта этого простейшего алгоритма, отличающихся тем, с какого разряда множителя - старшего или младшего начинается процесс, и тем, какие из чисел сдвигаются, а какие остаются на месте. Все эти варианты условно представлены на рис. 21.1.

Рис. 21.1
Первый вариант как раз соответствует примеру из предыдущей лекции. В этом варианте удвоение разрядности требуется только для аккумулятора и то лишь в случае работы без округления (целые числа или же так называемая двойная точность для мантиссы). Есть возможность вообще обойтись без отдельного регистра для младших разрядов произведения, если пересылать их при сдвиге в освобождающиеся разряды регистра множителя, как это показано на рисунке штриховыми линиями.
Во втором варианте удвоение разрядной сетки аккумулятора требуется всегда, независимо от наличия или отсутствия округления. Ведь если передавать старшие цифры произведения в регистр множителя С, то как быть с переносами, которые тоже должны туда передаваться. Переносы формируются и передаются только в сумматоре. Следовательно, не только аккумулятор, но и сумматор должен в этом варианте иметь удвоенную разрядную сетку.
В третьем варианте при работе без округления требуется удвоение разрядных сеток, как в аккумуляторе, так и в регистре множимого. При работе с округлением этот вариант дает увеличенную ошибку округления, так как здесь отбрасываются не только младшие цифры произведения, но и цифры множимого, а следовательно теряются возможные переносы из отброшенной части результата.
Четвертый вариант хуже всех остальных, так как он, при всех обстоятельствах, требует удвоения разрядных сеток двух регистров и сумматора. Между прочим, именно этот, наихудший для машинной реализации вариант соответствует обычному умножению "лесенкой".
По быстродействию все четыре варианта равноценны, все требуют выполнения
n циклов сложения и сдвига. На практике в основном применяется первый вариант, в отдельных случаях может быть использован второй.Многошаговая организация процесса умножения приводит к большим затратам времени. К так называемым "длинным" операциям машинной арифметики кроме умножения относится деление, но так как в среднестатистической смеси вычислительных работ умножение встречается примерно в 20 раз чаще, чем деление, то задача ускорения вычислений актуальна, прежде всего, именно для умножения.
Один из путей ускорения умножения состоит в группировке цифр множителя таким образом, чтобы в каждом цикле сложения и сдвига операцией цикла управляла бы не одна очередная цифра множителя, а две, три или даже четыре цифры. Соответственно можно было бы делать в каждом цикле сдвиг не на один разряд, а на два, три или четыре, и соответственно сократилось бы число циклов.
Рассмотрим простейший из этих алгоритмов с группировкой цифр множителя по две. В каждом цикле схема управления анализирует две младшие цифры множителя: С [1,0]. Эта пара цифр может иметь четыре значения, и соответственно возможны четыре ситуации:
В третьей ситуации удвоенное множимое легко получается сдвигом влево на один разряд. В четвертой ситуации нужно получить утроенное множимое то ли путем трехкратного сложения, то ли путем двух сложений: с множимым и с удвоенным множимым. Для ускоренного алгоритма это неприемлемо. Вместо этого делается вычитание множимого и запоминается необходимость в следующем цикле вернуть недостачу учетверенного множимого. Этот четверичный перенос в следующий цикл можно арифметически объяснить как использование в неявной форме четверичной системы счисления для множителя.
Каждый цикл заканчивается сдвигом на два разряда вправо множителя и суммы частичных произведений. Если все пары цифр множителя уже просмотрены, но недостача учетверенного множителя еще не возвращена, то делается еще раз прибавление множимого без последующего сдвига.
Вычитание модуля множимого, разумеется, происходит как прибавление дополнительного кода этого модуля, взятого со знаком "минус". Это обстоятельство в корне меняет отношение к "запасному" разряду слева в аккумуляторе. Если в описанном в предыдущей лекции алгоритме (будем называть его "базовым") роль "запасного" разряда произведения мог выполнять триггер переноса, то теперь на этом месте должна находиться знаковая цифра, так как в процессе формирования произведения знак А будет меняться. Знаковый разряд должен иметься и у сумматора. В свою очередь "запасной" разряд для хранения единицы переполнения тоже необходим. Поэтому нужно отвести под знаковые цифры по два разряда в регистре А и в сумматоре, т.е. использовать модифицированный дополнительный код.
В таблице 21.1 показаны все возможные сочетания младших цифр множителя с цифрой
T четверичного переноса и все соответствующие операции.Таблица 21.1

Схема микропрограммы умножения прямых кодов с группировкой разрядов множителя по два показана на рис. 21.2.
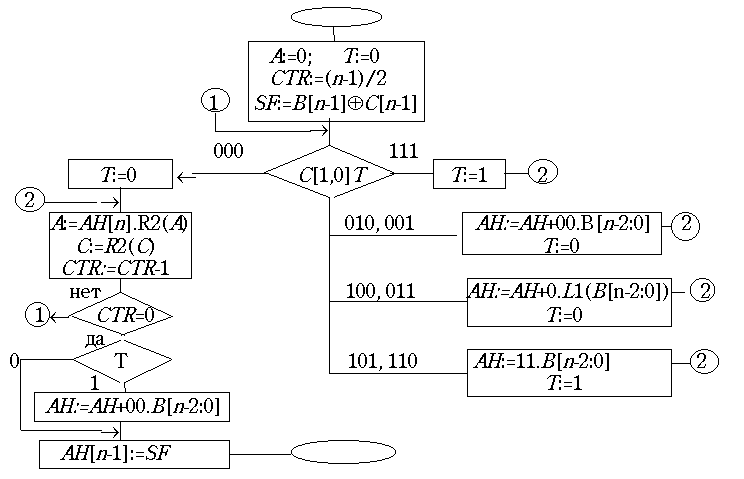
Рис. 21.2
При группировке цифр множителя по две сокращение времени счета всё же не получается двукратным. Как видно из таблицы 21.1, в шести случаях из восьми выполняется сложение, тогда, как в обычном алгоритме сложение выполняется примерно в половине всех циклов. Если считать все ситуации равновероятными, то в обычном алгоритме в каждом цикле выполняется в среднем 1,5 микрооперации (0,5 сложений и один сдвиг), а в алгоритме с группировкой цифр по две выполняется 6/8 +1 @
1,75 операции на цикл. Следовательно, на все циклы в обычном алгоритме приходится около 1,5n микроопераций, а при группировке цифр множителя - 1,75? n/2 @ 0,88n. Экономия времени составляет около 42%.Группировка цифр множителя по три или по четыре резко усложняет микропрограмму. В крупных ЭВМ третьего поколения, где мантиссы чисел с плавающей точкой представлялись в шестнадцатеричной системе, использовалась группировка цифр множителя по четыре. Предварительно вычислялись и запоминались в отдельных регистрах так называемые "кратные множимого", т.е. произведения модуля множимого на 2, 3 и 6. Эти "кратные" прибавлялись или вычитались из числа в аккумуляторе в зависимости от значения очередной тетрады множителя. В некоторых циклах приходилось выполнять до трех сложений. Из-за этого общая экономия времени по сравнению с простейшим алгоритмом составляла не более 35%.
Нужно сказать, что когда основание системы счисления равно целой степени двойки, и когда, следовательно, каждая цифра представлена двоичной диадой, триадой или тетрадой, для умножения годится любой из алгоритмов с группировкой двоичных разрядов множителя или без неё. Единственное требование, которое при этом необходимо строго соблюдать - это отсчет соответствующих групп от
q-ичной запятой.