20.
Сложение и умножение двоичных чисел (лекция 20)В дальнейшем при описании алгоритмов выполнения арифметических операций в процессоре мы будем пользоваться языком функционального микропрограммирования или "Ф-языком". Примеры выражений этого языка:
С
:=R 2(С) -логический сдвиг на два разряда вправо в регистре С,В
:=В[n-1].L1(B).0 -арифметический сдвиг дополнительного кода в регистре В на один разряд влево,А
:=С -пересылка числа из регистра С в регистр А,![]()
Язык функционального микропрограммирования очень прост и гибок, позволяет с помощью оператора присваивания записывать любые элементарные действия над числами. Сами числа своих наименований не имеют, под числом подразумевается содержимое определенного регистра.
Ниже мы будем придерживаться следующих обозначений регистров или регистровых пар: В и С
- регистры - источники, А - аккумулятор, т.е. регистр, непосредственно связанный с выходом сумматора. Результат операции обычно помещается на место первого операнда, но это происходит лишь в конце операции, поэтому ради простоты описания алгоритмов эту заключительную пересылку можно не описывать.Рассмотрим сложение
A := В + С. Допустим, что числа загружаются в процессор и выгружаются из него в дополнительном коде. Алгебраическое сложение чисел при этом происходит проще, чем при использовании прямого кода. Существуют два варианта организации сложения: одноадресный и двухадресный.При одноадресном способе на одно и то же "плечо" сумматора сперва подается первое слагаемое В, а затем второе С. Результат помещаются в аккумулятор А (рис.
20.1).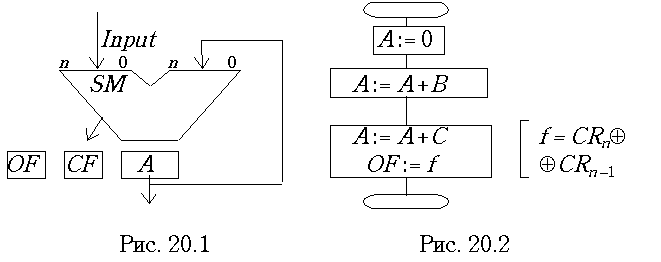
Рис. 20.2 показывает микропрограмму одноадресного сложения. Признак переполнения
f здесь получается сложением по модулю 2 двух величин переноса: в знаковый разряд и из него. Логический способ контроля переноса путем сопоставления знаков операндов и знака результата здесь невозможен, так как знаковые цифры слагаемых не могут быть прочитаны одновременно.На рис. 20.1 и 20.2, как и в дальнейшем, применены обычные обозначения признаков результата (флагов) и логических переменных.
OF – флаг переполнения, CF – флаг переноса, CR – перенос как логическая переменная или сигнал на линии связи. Флаги представляют собой просто триггеры, связанные со схемой управления арифметическими операциями.Двухадресное сложение (рис.20.3) дополнительных кодов проще одноадресного. Здесь операнды одновременно подаются на два входа сумматора, предварительное обнуление аккумулятора не требуется. Схема микропрограммы показана на рис 20.4. В ней принят логический способ контроля переполнения.

Посмотрим, насколько усложнится алгоритм сложения, если числа в регистрах В и С, а также окончательный результат находятся в прямом коде.
При одноадресном сложении знаковая цифра очередного операнда анализируется схемой управления. Если это нуль, то выполняется операция сложения этого операнда с содержимым аккумулятора (к началу операции он должен быть обнулен!). Если же знаковой цифрой является единица, то происходит сложение с обратным кодом операнда, который считывается с инверсных выходов соответствующего регистра. Чтобы обратный код превратить в дополнительный, в младший разряд сумматора нужно добавить единицу. Эта единица поступает по входу переноса в младший разряд.
По двухадресной схеме сложение чисел с одинаковыми знаками можно делать без обращения кода. При этом складываются модули, а знак суммы определяется логически. При несовпадении знаков слагаемых отрицательный операнд переводится в дополнительный код. При этом алгоритме сложения у сумматора отсутствует знаковый разряд. При сложении чисел с одинаковыми знаками триггер переноса
CR контролирует переполнение, а при сложении чисел с противоположными знаками он определяет знак суммы. Ведь при сложении в дополнительном коде чисел с противоположными знаками перенос из старшего разряда получается, если сумма положительна или равна нулю. Контроль переполнения в случае противоположных знаков слагаемых не требуется.Схема микропрограммы при двухадресном сложении получается сложнее, ввиду большего числа проверок логических условий, зато необходимое число последовательно выполняемых операций заметно сокращается. Микропрограммы сложения по обоим описанным способам приведены на рис. 20.5 (одноадресный вариант) и рис.20.6 (двухадресный вариант).
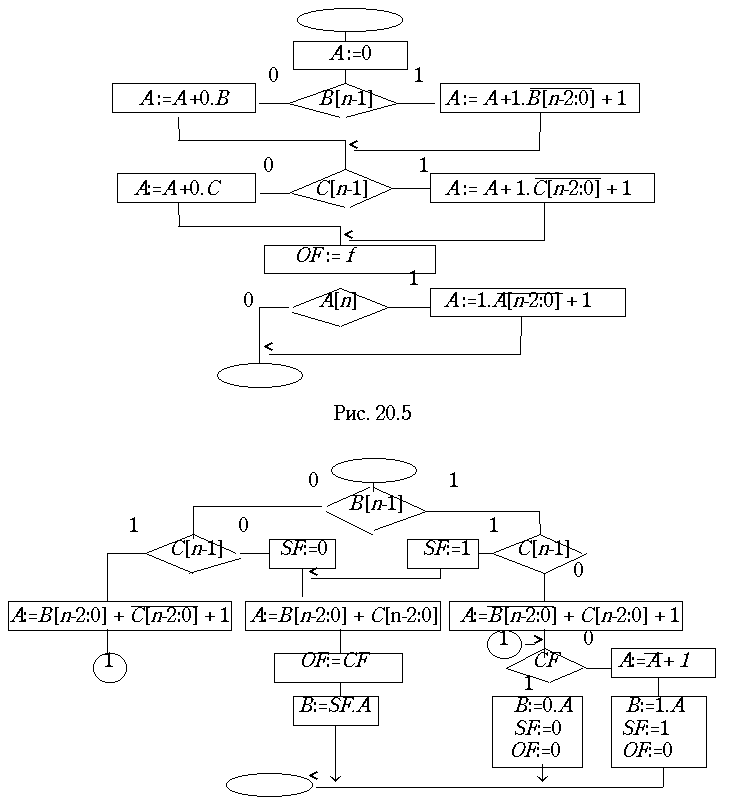
Рис. 20.6
На рис. 20.6 показаны заключительные операции пересылки результата в регистр B и установки знакового флага SF.Описанные алгоритмы сложения прямых кодов в общих чертах сохраняются при сложении десятичных чисел или мантисс чисел с плавающей точкой. Как одни, так и другие загружаются в процессор и выгружаются из него в прямом коде, поэтому схема, показанная на рис. 20.6, как правило, входит в качестве основного модуля в относительно более сложные схемы микропрограмм сложения десятичных чисел или чисел с плавающей точкой.
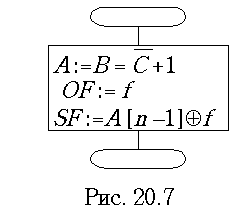
Арифметическая операция вычитания сводится к алгебраическому сложению, т. е. второй операнд берется с обратным знаком. Схема микропрограммы вычитания дополнительных кодов показана на рис. 20.7. В ней указан способ верной установки флага знака результата даже при переполнении.
Умножение в ЭВМ заменяется рядом последовательно выполняемых операций сложения и сдвига. При умножении вручную "лесенкой" мы суммируем сразу все частичные произведения насквозь. Машина так работать не может. Понадобилось бы слишком много регистров для хранения частичных произведений, да и складывать сразу несколько чисел обычный сумматор не может. Поэтому каждое очередное частичное произведение машина сразу прибавляет к полученной до того сумме частичных произведений.
Таким образом, произведение накапливается постепенно в регистре сумматора, в связи с чем этот регистр и называют аккумулятором.Поясним сказанное примером. Воспользуемся принятыми ранее обозначениями кодов: угловые скобки для прямого кода. Умножим 12 на –13 в прямом коде.
Каждый цикл заканчивается сдвигом суммы частичных произведений и модуля множителя на один разряд вправо. Последовательность операций поясняет таблица 20.1.
В таблице множитель показан без знакового разряда, так как этот разряд в операциях цикла не участвует. При сдвиге младшие цифры множителя теряются, они больше не нужны. Регистр-аккумулятор имеет двойную длину для сохранения младших разрядов, которые иначе были бы потеряны при сдвигах. При перемножении целых чисел (как в нашем примере) двойной формат произведения обязателен. Если же числа являются дробями и могут округляться (мантиссы чисел с плавающей точкой), то удвоение формата произведения не обязательно, но может иногда делаться для повышения точности вычислений. Произведение, как показано в таблице, имеет один разряд слева, который не участвует в сложениях и не является знаковым разрядом. Этот добавочный разряд необходим для временного хранения единицы переполнения разрядной сетки произведения. Роль этого разряда обычно играет триггер переноса СF. Комбинационный сумматор в этом случае имеет n-1 разряд, как и при сложении прямых кодов по алгоритму на рис. 20.6.Табл. 20.1
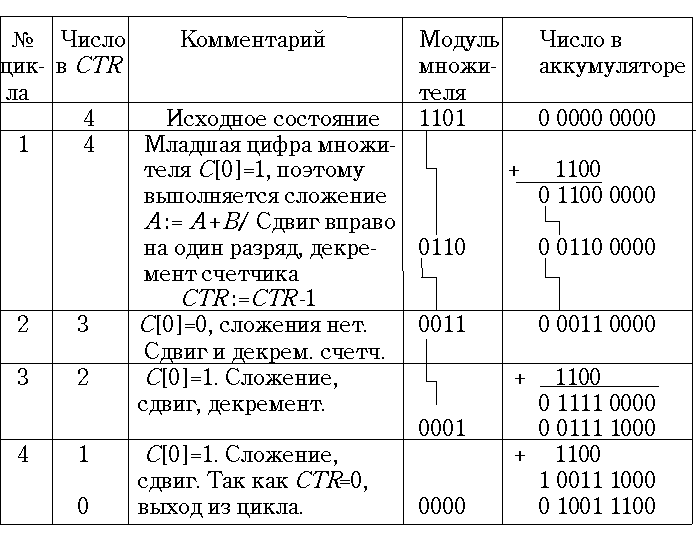
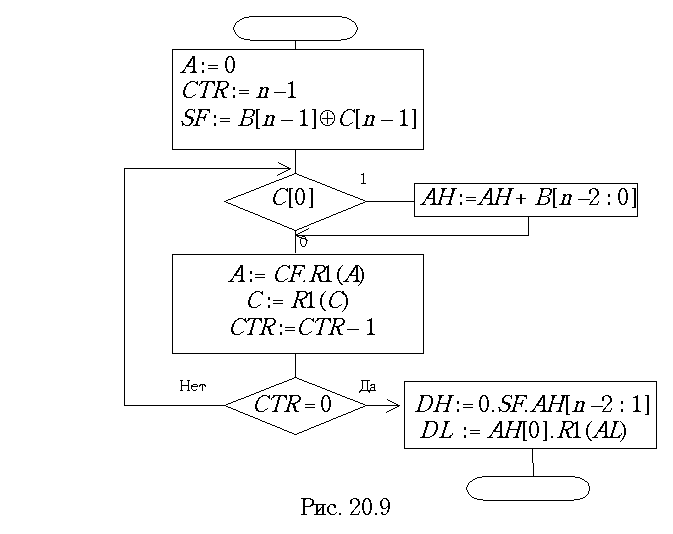
Сдвиг чисел А и С происходит как сдвиг кода. В конце микропрограммы умножения целых чисел результат может быть помещен в пару регистров общего назначения, имеющих стандартную длину
n. Назовем эти регистры DH и DL . Чтобы представление целого числа в формате двойной длины было правильным, перед пересылкой нужно выполнить еще один сдвиг вправо, как показано на рис. 20.8.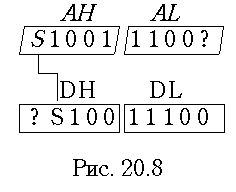
В регистре
AL младший разряд в процессе умножения не участвовал и в таблице не был показан. На рис. 20.8 он обозначен знаком вопроса. Однако перед выгрузкой числа двойной длины из аккумулятора делается еще один сдвиг вправо, в результате чего неиспользуемой цифрой становится старшая цифра регистра AH. Не следует смешивать это представление числа, которое возможно только в двойном формате, с модифицированным кодом, так как модифицированный прямой код не имеет смысла и не применяется.На рис. 20.9 показана схема микропрограммы умножения прямых кодов, соответствующая рассмотренному примеру.