18

18. Кодирование отрицательных чисел (лекция 18)

прямой код,
дополнительный код,
обратный код,
кодирование правильных дробей

Числа с фиксированной точкой и мантиссы чисел с плавающей точкой могут участвовать в машинной арифметике в одном из трех кодов: прямом, дополнительном или обратном. Дадим определения этих кодов для целых двоичных чисел. Общее число разрядов, включая знаковый, будем обозначать буквой n. Нумерация, согласно общепринятому правилу, начинается с нуля. Таким образом, разряд с весом будет являться знаковым. Для упрощения записей будем пользоваться следующими обозначениями:

|A| -модуль числа A;

- прямой код того же числа;

- дополнительный код того же числа;

- обратный код того же числа.

Прямым кодом числа А называется запись

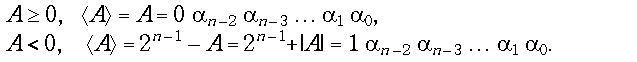
Прямой код совпадает с записью числа в определенной нами ранее естественной форме. Число - 1010 в прямом коде запишется как 11010. В этом коде нуль имеет два значения: + 0 = 0000.....0 и - 0 = 1000.....0.

В этом коде можно складывать числа, имеющие одинаковые знаки. При этом знаковые цифры не складываются, как все остальные, знак суммы определяется отдельной логической операцией. Переносы в знаковый разряд не допускаются. Примеры сложения чисел в прямом коде:

Выделенные нами знаковые цифры результата получаются логически, т.е. результату присваивается тот же знак, что у слагаемых. Сложение знаковых цифр недопустимо, так как оно ведет к неправильному результату. Во втором примере получилось бы 1+1=10, единица переноса была бы потеряна, а в знаковом разряде остался бы нуль.

При вычитании или, что то же самое, при сложении чисел с противоположными знаками пришлось бы реализовать очень сложный алгоритм. Сперва каким-то путем устанавливать, какое из слагаемых имеет больший модуль (например, с помощью специальной комбинационной логической схемы) и запоминать его знак, затем из большего модуля вычитать меньший. Практически это никогда не делается, просто прямой код не используется для алгебраического сложения, то есть для сложения чисел с произвольными знаками.

Дополнительным кодом называется запись:

Член вне скобок - это единица знакового разряда, а внутри скобок находится дополнение модуля числа A до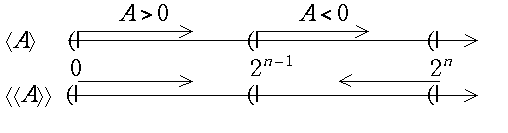 . Сравним графические представления чисел в прямом и дополнительном кодах (рис. 18.1).

Рис. 18.1

Стрелки указывают направление увеличения модуля, скобки определяют, каким сегментам принадлежат граничные точки. Из рисунка видно, что в дополнительном коде, как и в прямом, для изображения отрицательных чисел выделен отрезок положительной числовой оси. Отличие состоит в том, что в дополнительном коде отсчет на этом отрезке идет справа налево.

Дополнение модуля числа до теоретически определяется вычитанием. Например: n = 6; А = - 00101. Вычтем модуль A из

Находить дополнение вычитанием в машинной арифметике нельзя, так как вычитание в обычном смысле этого слова вообще не используется. Машинный алгоритм основан на преобразовании:

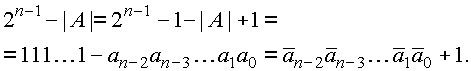
Поразрядное вычитание двоичных цифр из единицы равносильно их инвертированию как логических переменных, что выполняется очень просто. Чтобы преобразовать прямой код отрицательного числа в дополнительный, нужно, не меняя знаковой цифры, проинвертировать цифры модуля и прибавить единицу. Для обратного перехода, казалось бы, требуются противоположные действия, т.е. сперва отнять единицу, а потом проинвертировать цифры дополнения. Однако точно такой же результат получается при повторном применении прямых действий: инверсия и плюс единица. Дело в том, что вычитать единицу из дополнения или прибавлять единицу к модулю - это равносильные операции.

В дополнительном коде нуль имеет только одно значение: “плюс нуль”. Попытаемся получить “минус нуль”

+1 = 111111+1 =

Выделенная рамочкой единица выходит из разрядной сетки и теряется. В пределах принятого формата числа остается код “плюс нуля”.

В дополнительном коде сложение и вычитание выполняются одинаково, как алгебраическое сложение чисел с произвольными знаками. При этом знак суммы получается арифметическим путем, благодаря распространению сложений и переносов на знаковый разряд. Рассмотрим сложение при разных сочетаниях знаков слагаемых В, С и суммы А.

1) В > 0, С > 0. Этот вариант выполняется как в обычной арифметике и внешне - как в прямом коде, но знак суммы определяется сложением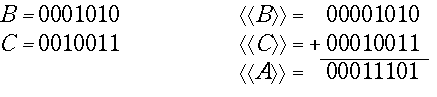

2) В > 0, C < 0, |A| > |C|. Этот вариант равносилен вычитанию положительного С :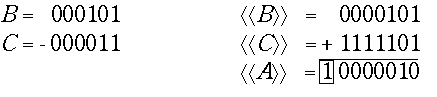

Заключенная в рамку единица переноса из старшего разряда суммы теряется. Ее потеря не является ошибкой. Дополнительный код отрицательного числа по определению отличается от истинной величины числа на константу, равную . При получении положительной суммы эта константа оказывается лишней и должна исчезнуть;

3) В > 0, C < 0, |B| < |C|.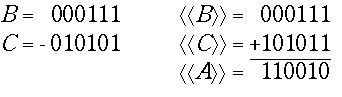

4) В < 0, C < 0. В этом варианте для формирования кода отрицательного числа требуется одна константа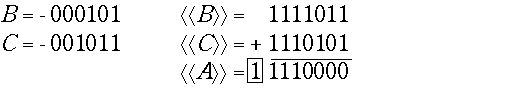 , а поступают со слагаемыми -две. Одна из них должна исчезнуть.

Обратным кодом называется запись: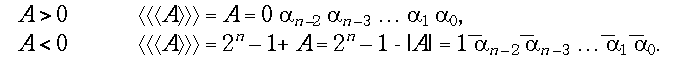

Обратный код отличается от дополнительного отсутствием единицы, прибавляемой после инвертирования. Эту отсутствующую единицу иногда приходится прибавлять искусственно, чтобы скорректировать результат сложения. В обратном коде нуль имеет два значения: “плюс нуль” 0000....0 и “минус нуль” 1111...1. Сложим в обратном коде числа с разными сочетаниями знаков:

1) В > 0, C > 0. Этот случай в любом коде выполняется одинаково.

2) В > 0, C < 0, |B| > |C|.

Объясним причину необходимости так называемого “циклического переноса”. В коде отрицательного слагаемого недоставало единицы младшего разряда (по определению кода). Сумма получилась положительной, а здесь по определению прямого кода недостача единицы не предусмотрена. Следовательно, эту единицу следует прибавить искусственно. Признаком данной ситуации является перенос из старшего разряда суммы, который уносит константу, входившую в код отрицательного слагаемого. “Циклический перенос”, это - всего лишь мнемонический прием, означающий, что если при сложении обратных кодов произошел перенос из знакового разряда, то необходимо скорректировать сумму.

3) В > 0, C < 0, |B| < |C|.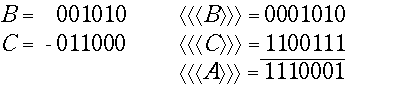

4) B < 0, C < 0.

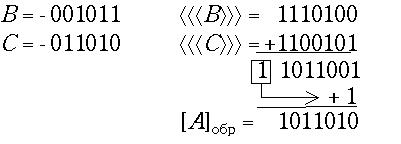
Правильные двоичные дроби в прямом, дополнительном и обратном кодах изображаются подобно целым числам, но в определении кодов используются другие константы:

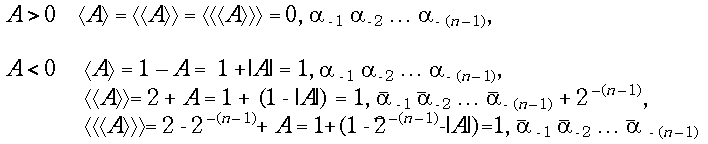
В заключение этой темы запишем определения прямого, дополнительного и обратного кодов для целых чисел при произвольном основании системы счисления q.

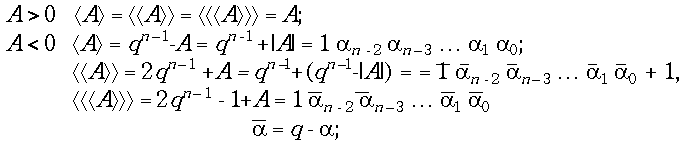
Обратим внимание на то, что здесь при формировании дополнительного и обратного кодов инвертирование цифр определяется как арифметическое дополнение до старшей цифры в данной системе.

Для правильных дробей определения прямого, дополнительного и обратного кодов описываются следующими выражениями:

Содержание