
17.
Представление чисел в машинах (лекция 17)Число в так называемой естественной форме, это - обычная позиционная запись в принятой системе счисления. Число считается целым, т.е. запятая условно фиксируется справа от младшего разряда числа. Старшая цифра числа изображает знак: “плюс” кодируется цифрой нуль, а “минус” - единицей. Общее число разрядов, включая знаковый, мы будем обозначать буквой n, причем это число будем считать постоянным. Дело в том, что для записи чисел, для их параллельной пересылки и т.п. используется аппаратура, количество разрядных модулей в которой остается постоянным, вследствие чего и длина числа должна оставаться постоянной (за некоторыми исключениями). Оно должно вписываться в так называемый “формат числа” или “разрядную сетку”, представление о которой дает рисунок 17.1.

Рис. 17.1
Определим диапазон чисел, представляемых в естественной форме. Допустим, что система счисления - двоичная, а
n = 32. Таков один из стандартных форматов для двоичных чисел. Модуль числа изображается n - 1 цифрой, следовательно, самым большим числом будет число, изображающееся 31 единицей. Наименьшим (не равным нулю) числом будет очевидно единица. Ширину диапазона определяет отношение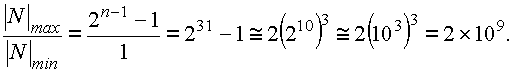
Эта величина не так уж велика для машинной арифметики. Число
N не должно выходить из названного диапазона. Если оно окажется больше, чем |N|max,, произойдет грубая ошибка - ошибка переполнения, при которой теряется более половины величины числа в соответствии с весом цифры, вышедшей из разрядной сетки влево.Если число окажется меньше единицы, то в разрядной сетке останется изображение нуля, тогда как число может быть принципиально отличным от нуля по смыслу задачи (например, при делении чисел). Вообще целочисленный результат во многих вычислительных задачах получается после округления смешанной дроби. Максимальное значение абсолютной ошибки округления до целого числа составляет
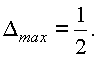
Так называемая “действительная” относительная ошибка округления определяется как абсолютная ошибка, отнесенная к модулю округляемого числа. Максимальная величина её равна
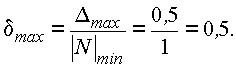
Чтобы застраховаться от ошибок переполнения и не допускать слишком больших ошибок округления, диапазон представляемых чисел приходится искусственно суживать. В результате практически используемый диапазон получается небольшим, что является принципиальным недостатком чисел с фиксированной точкой.
В полулогарифмической форме число определяется формулой
![]() ,
,
где М -нормализованная мантисса,
q
-основание системы счисления (во всяком случае, для мантиссы),Е -порядок числа.
Числа в полулогарифмической форме (числа с плавающей точкой) могут иметь разную длину, но мы возьмем такую же длину, какую принимали для чисел в естественной форме: 32 разряда. Такую длину имеет один из форматов чисел персональной ЭВМ - формат КВ (“короткое вещественное”). В нем принята двоичная система, условие нормализации имеет вид
![]()
При этом условии нормализованная мантисса не может быть меньше единицы и представляет неправильную дробь с единицей слева от запятой. Ввиду того, что эта единица имеется обязательно, её можно не записывать в изображение числа, а лишь подразумевать. Представление числа в формате КВ показано на рис. 17.2.
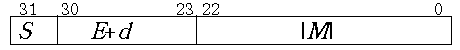
Рис. 17.2
Старшая цифра
S кодирует знак числа, затем идет восьмибитовое поле, называемое характеристикой, а затем следуют 23 цифры модуля мантиссы без единицы целой части. В таком виде число с плавающей точкой пересылается по шинам данных и хранится в памяти машины. Для участия в арифметических действиях число переводится в так называемый внутренний формат арифметического сопроцессора, где старшая цифра мантиссы присутствует явно. Об этих деталях будет сказано позже, при рассмотрении форматов всех чисел ПЭВМ.Е
+d - характеристика , в которой содержится константа d, называемая “смещением”. В формате КВ смещение составляет d = 127. Самое маленькое число, которое можно записать в восьми разрядах характеристики равно нулю, а самое большое равно 255. Эти два числа: самое большое и самое маленькое, предназначаются для кодирования особых ситуаций, поэтому их нужно исключить из нашего расчета. Следовательно, в поле характеристики могут быть заданы величины порядка Е: от 1 - 127 = --126 до 254 - 127 = 127. Определим диапазон чисел, представимых в формате КВ: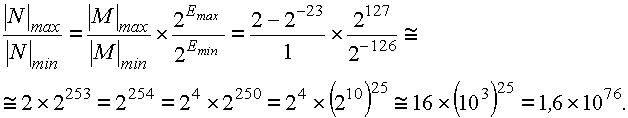
Это уже очень большая величина, достаточная для любых расчетов научно-технического характера. Определим ошибку округления. Для нормализованных мантисс она составит:
![]()
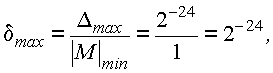
Что в переводе в десятичную систему приблизительно равно
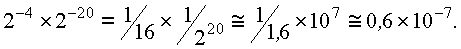
Ошибка достаточно мала - меньше одной десятимиллионной. Преимущества полулогарифмической формы очевидны. Она является основной формой для научных и технических расчетов (даже в карманных калькуляторах), незаменима в машинной графике, но и естественная форма имеет свою область применения.
Десятичные числа в машинах представляются в естественной форме. Исключением являются калькуляторы, которые работают с десятичной системой, как в естественной, так и в полулогарифмической формах. Для универсальной ЭВМ десятичная арифметика является вспомогательным средством, а также используется при вводе и выводе. Многие специализированные бухгалтерские (кассовые, фактурные и т.п.) машины работают только с десятичными числами. У таких машин очень велик объем входных и выходных данных, при предельной простоте алгоритмов обработки. В связи с этим нецелесообразно переводить числа из десятичной системы в двоичную, а затем обратно.
При вводе десятичных цифр с клавиатуры, при выводе на печать или при записи на магнитный носитель используется так называемый “зонный” формат, когда каждой цифре соответствует один байт (рис. 17.3).
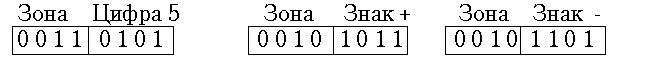
Рис. 17.3
Старшая тетрада означает номер колонки кодовой таблицы и указывает, что байт содержит именно цифру, а не другой символ. Знаки “плюс” и “минус” тоже кодируются отдельным байтом, но в некоторых случаях знаковая тетрада может занимать место зонной у младшей из передаваемых цифр числа. Заметим, что на рис. 17.3 даны изображения в соответствии с кодом КОИ-8 или международным кодом ASCII (American Standard Code for Information Interchange). Существуют и другие широко распространенные кодовые системы, в частности наш ДКОИ (двоичный код для обмена информацией), соответствующий международному коду EBCDIC (Expanded Binary Coded Decimal Interchange Code). Здесь для цифровой тетрады зона содержит код 1111, “плюс” изображается байтом 0100 1110, а “минус” - 0110 1101
При выполнении арифметических операций над десятичными числами по последовательному алгоритму, т.е. не более, чем по одной цифре за один шаг, зонный формат используется не только для пересылки чисел при вводе и выводе, но и непосредственно для их обработки. Именно так выполняется умножение и деление десятичных чисел в персональной ЭВМ. В машине, специализированной на выполнении десятичных операций, перед началом обработки числа переводятся в упакованный формат со знаковой тетрадой справа от младшего разряда или слева от старшего.
Упакованный формат используется для преобразования чисел в двоичную систему счисления и обратно, или непосредственно применяется в вычислениях.