16.
Позиционные системы счисления (лекция 16)Позиционная запись числа A подразумевает его представление в виде суммы
![]()
где
n = k + m
Фактически число записывается как ряд цифр, а для указания начала отсчета степеней основания системы служит
q-ичная запятая или “точка”.Общие принципы арифметики в любой из позиционных систем одинаковы. Различия сводятся к неодинаковому количеству используемых цифр. Чем больше допустимых цифр, тем больше получается парных сочетаний этих цифр в элементарных операциях. В десятичной арифметике таблицы элементарных операций сложения или умножения имеют размер 10х10 = 100, а в шестнадцатеричной - 16х16 = 256.
Самые простые правила у двоичной арифметики. Таблицы сложения и умножения имеют размер 2х2, причем функция суммы двух цифр совпадает с логической функцией неравнозначности, а функции переноса и произведения одинаковы и совпадают с конъюнкцией. В результате действия над многоразрядными числами тоже оказываются очень простыми. Примеры:
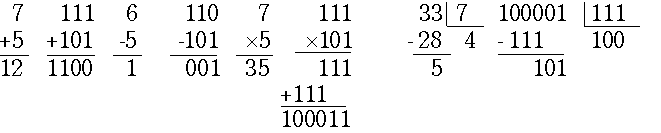
Особенно заметное упрощение получается при умножении и делении чисел. Умножение превращается в ряд сдвигов и сложений, а при делении не приходится подбирать очередную цифру частного - вычитание то происходит, то не происходит.
Простота правил арифметики, сводимость элементарных операций к функциям булевой алгебры и, наконец, легкость технической реализации двоичных сигналов и записи двоичных кодов на любых носителях информации - вот причины исключительного применения двоичной системы в современных ЭВМ.
При
q > 2 действия намного усложняются. При выполнении операций “вручную” каждое элементарное действие приходится разбивать на два шага. Складывая две цифры, мы сперва в уме находим сумму по правилам десятичной арифметики, затем переводим её в систему счисления с заданным основанием и только после этого делаем соответствующую запись. Аналогично действуем при умножении. Сперва две цифры перемножаются в уме в десятичной системе, затем к результату (в уме) прибавляется перенос. Только после этого результат перемножения двух цифр переводится в нужную систему.Примеры:

Из систем с основанием, отличным от 2, основной интерес представляют две системы: десятичная и шестнадцатеричная. Первая из них необходима, по крайней мере, для ввода и вывода чисел, а вторая, как и другие системы с основанием, кратным целой степени двойки, обладает определенными преимуществами перед другими системами. По сравнению с двоичной системой запись числа в шестнадцатеричной системе гораздо компактнее, так как одна шестнадцатеричная цифра заменяет тетраду двоичных цифр:
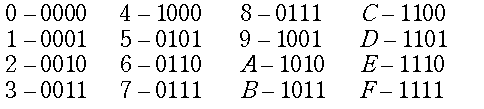
Шестнадцатеричная система не создает никаких проблем для машинной арифметики, так как при сложении и вычитании сохраняются правила двоичной арифметики. Фактически в сложении участвуют двоичные эквиваленты шестнадцатеричных чисел. Пример:
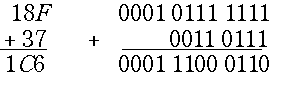
Десятичные числа в машине тоже заменяются двоичными тетрадами, но правила арифметики получаются гораздо более сложными. Они будут рассмотрены позже, а сейчас перейдем к вопросу о переводе чисел из одной системы счисления в другую.
Проще всего этот вопрос решается, если у обеих систем: “старой” и “новой” основание равно целой степени двойки. При этом для перевода чисел достаточно в качестве промежуточной формы записать двоичный эквивалент, а затем перегруппировать разряды по-новому, начиная от запятой вправо и влево. Переведем восьмеричное число 35,3 в шестнадцатеричную систему:
![]()
Описанное преобразование является частным случаем. В более общем случае перевод выполняется с помощью специального вычисления. Из определения позиционного числа вытекает формула для преобразования целых чисел из системы с основанием
p в систему с основанием q:![]()
Этой формуле соответствует следующий алгоритм преобразования
(все действия выполняются по правилам q–ичной арифметики):Для правильных дробей аналогичное по смыслу преобразование задает формула:
![]() .
.
Соответствующий алгоритм в словесном описании:
Заметим, что выполнение указанных действий неизбежно связано с округлением результата. Все действия описанных алгоритмов выполняются по правилам арифметики с “новым” основанием.
Существуют также алгоритмы, противоположные описанным. Для целых чисел:
Переведем по этому алгоритму десятичное число 106 в троичную систему:
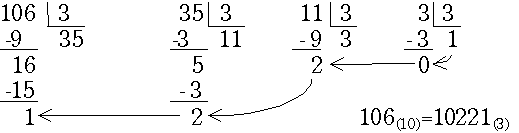
Для правильных дробей этот вариант алгоритма будет формулироваться следующим образом:
Переведем по этому способу в десятичную систему двоичную дробь 0,00111101 с точностью до двух значащих цифр:
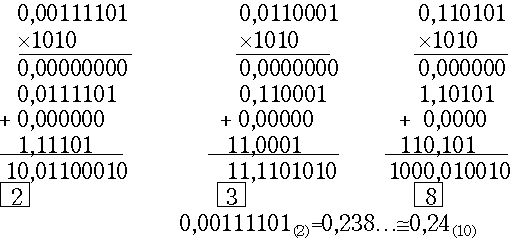
Если число является смешанной дробью, то при любом варианте алгоритма его нужно переводить по частям: целую и дробную части по отдельности с последующим объединением результатов.