14.
Элементы
математической логики. Исчисление высказываний
(лекция 14)
- определение формальной теории,
- гильбертово исчисление высказываний,
- сравнение с алгебраическим подходом.
Исчислением или формальной
теорией принято называть некоторую
совокупность понятий и правил, позволяющую
решать определенный класс задач. Такое общее
определение расплывчато и интуитивно, но каждое
конкретное исчисление формулируется предельно
строго. При этом не принято сообщать о возможных
практических применениях того или иного
исчисления - этот вопрос остается открытым.
Каждый может решать его по-своему, применительно
к своим задачам.
Исчисление высказываний (ИВ)
составляет основу математической логики. Оно
определяет способы получения верных
умозаключений из заданных высказываний A, B, C,... В основу
ИВ кладется требование, чтобы его собственные
построения, формулируемые в общем виде, были
истинными независимо от истинности А, В, С, ...
Получение истинных высказываний при ложных
предпосылках, вообще говоря, возможно (если "х"
- ложно, значит "не х" - истинно). ИВ
интересуют именно такие, тождественно-истинные
высказывания, которые называются тавтологиями.
Они то и позволяют находить верные заключения
при любой истинности посылок. ИВ строится
следующим образом:
- Задается алфавит ИВ. Он содержит:
- символы А, В, С, ..., обозначающие простые
высказывания, значения которых принадлежат
множеству { 0,1}
. Они знакомы нам как
булевы переменные в алгебре логики. В ИВ они
называются пропозициональными буквами, т.е.
буквами предложений;
- символы логических операций, принятых в данном
ИВ, например ®, &, U и т.п. Здесь
они называются пропозициональными связками,
т.е. предлогами;
- вспомогательные символы: скобки и запятая;
- Определяется множество выражений, допустимых в
ИВ, т.е. формул. Из-за бесконечности множества
формул его приходится задавать с помощью
рекурсии:
- входная часть: "Пропозициональная буква есть
формула";
- циклическая часть: "Если А и В формулы,
то (А&В), (А Ъ В), (А ®
В) тоже формулы".
Из этого определения следует, например, что ((АЪВ) ® (С&D)) - тоже
формула. Рекурсия позволяет строить
бесчисленные формулы путем их композиции.
Внешние скобки у формул часто не используют, если
это не ведет к ошибкам;
- Из множества формул выделяются те, которые
объявляются аксиомами данного ИВ. Аксиома
непременно должна быть тавтологией, например ((a
& b ) ® a), a
Ъ `a, ((a & (a ® b )) ® b ) и т.п.
- Из аксиом выводится несколько отношений между
формулами. Они называются правилами вывода и
изображаются записью вида
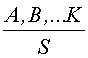 ,
,
которая понимается
так: "если все формулы над чертой истинны, то S
истинно". Формулы над чертой называются посылками
или гпотезами, а символ под чертой - логическим
заключением.
Формальное решение логической задачи
сводится к подбору подходящего правила вывода,
чтобы над чертой оказались только имеющиеся
истинные посылки или непосредственно из них
вытекающие формулы, а под чертой оказалась бы
такая формула S, которая удовлетворяла бы нас в
качестве ответа на задачу.
Приведем пример. Примем гильбертово
ИВ, в котором определены связки: &,
Ъ, `x и ® .
Примем условия задачи: "Известно, что в корзину
помимо всего прочего положили яблоко. Известно
также, что или в корзине нет яблока, или там есть
помидор. Доказать, что в корзине есть помидор".
Обозначим:
"В корзине есть яблоко" - А
;
"В корзине есть помидор" - В
.
Будем искать подходящее правило
вывода и подгонять под него имеющиеся посылки. В
гильбертовом исчислении используется правило отделения
заключения от
посылки или modus ponens, известное еще со времен
Аристотеля:
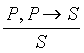 .
.
Произведя эквивалентное преобразование (
`А Ъ В ) 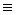 (А ® В
) приводим задачу к желаемому виду
(А ® В
) приводим задачу к желаемому виду 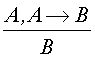 .
.
В других исчислениях применяются и другие
правила вывода:
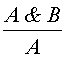 ,
, 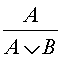 и т.п. Общее число правил вывода
может быть как угодно большим, так как однажды
доказанное отношение может затем многократно
применяться как установленное правило.
и т.п. Общее число правил вывода
может быть как угодно большим, так как однажды
доказанное отношение может затем многократно
применяться как установленное правило.
Рассмотренный пример можно было бы
решить алгебраически. Даны две посылки: А
= 1; ` А Ъ В=1. Так как
посылки верны, должна быть верна и их конъюнкция А ( `АЪВ ) = 1. Подставим А = 1 и тогда 1(0 Ъ В ) = 1; 0 Ъ В =
1; В=1. Алгебраический
способ может показаться более простым для
человека, привыкшего к алгебраическим задачам.
Но алгебраический подход для логики
недостаточно строг, так как некоторые действия
при нем выполняются интуитивно. В рассмотренном
примере мы не приравняли `А U В=1 согласно условия,
а подставили только А = 1. Почему? Это было сделано,
чтобы избежать тождества 1=1. Интуитивно был
выбран более удачный путь, но мы даже не подумали,
имеем ли мы право подставить одно тождество и не
подставить другого!
Способ доказательства в ИВ отличается
явной фиксацией всех действий, в том числе и
таких, которые по отношению к алгебраическим
операциям являются внешними, самой алгебре не
принадлежащими. Запись правила вывода не
является формулой, хотя её хочется понимать
именно так. Это
метаформула, фиксирующая определенный
шаг умозаключений. В алгебрах метаформул нет, их
заменяет соответствующий словесный комментарий,
всё равно необходимый в любой прикладной
области, где та или иная алгебра используется.
В исчислениях принципиально не
пользуются словесными комментариями, так как их
справедливость невозможно проверить
формальными средствами. Отсутствие словесного
комментария оказывается объективной
необходимостью.
Содержание
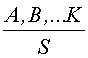 ,
,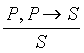 .
.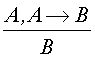 .
.
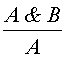 ,
, 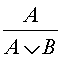 и т.п. Общее число правил вывода
может быть как угодно большим, так как однажды
доказанное отношение может затем многократно
применяться как установленное правило.
и т.п. Общее число правил вывода
может быть как угодно большим, так как однажды
доказанное отношение может затем многократно
применяться как установленное правило.