13.
Примеры комбинаторных задач (лекция 13)Правило умножения, использованное нами для вывода нескольких формул, является самым простым, но не всегда применимым способом. Рассмотрим задачу, требующую более сложного метода решения.
Определим мощность булеана
![]() = {
= {
{ an - 1, an } , ......... { an-2, an-1, an } , ...{ a1, a2, ...an } } .
Как определить
{ a1, a2, a3 } , число элементов в таком множестве? Допустим, что элемент аn исключен из А. При этом из булеана исчезнут все выборки, содержащие аn. А их ровно столько же, сколько останется после исключения аn. Ведь исключенные выборки могут быть получены присоединением аn к каждой из оставшихся выборок. Следовательно, уменьшение числа элементов с n до n-1 уменьшает мощность булеана вдвое, что можно записать так:![]()
Мы получили рекуррентное (возвратное) соотношение, т.е. выразили решение задачи с
n элементами через решение аналогичной задачи с меньшим числом элементов. Применяя это соотношение последовательно к ряду булеанов с понижающимся числом n, получим![]()
Примененный способ вывода или доказательства теорем интересен своей своеобразностью и эффективностью. Что касается мощности булеана, то её можно было бы определить и более простыми, хотя и менее строгими способами. Например, можно доказать, что
![]()
Затем доказать, что правая часть равенства представляет сумму элементов одной строки треугольника Паскаля. Ввиду того, что в треугольнике Паскаля каждый элемент является суммой двух вышележащих, сумма членов с каждой новой строкой удваивается. Вследствие этого за
n шагов получается сумма, равная 2n.Другой, еще более простой способ: можно противопоставить каждому из составляющих булеан подмножеств
n-разрядное двоичное число, где единица заменяет соответственный элемент Аi , присутствующий в подмножестве, а нуль - отсутствующий элемент. Тогда общее число n- разрядных двоичных чисел определится как число размещений с повторениями, т.е. как 2n.Над комбинаторными конфигурациями можно выполнять преобразования, описываемые средствами специальных алгебр. Возьмем один уже знакомый нам вид конфигураций: перестановки, т.е. кортежи длины
n, составленные из неповторяющихся элементов, число которых тоже равно n. Будем обозначать перестановки буквой П с порядковыми индексами. Допустим П1 = (1, 2, 3); П2 = (1, 3, 2) ...Подстановкой назовем унарную операцию, позволяющую получить одну перестановку из другой. Например, подстановка a выполняет преобразование П
1 в П2 или П2 = a (П1). Подстановки задают сопоставлением двух кортежей в общей паре скобок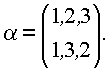
или с помощью диаграммы (рис.13.1).
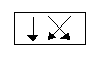
Рис. 13.1
Верхний кортеж в паре скобок называют операндом, а нижний - результатом подстановки. Из свойств подстановки очевидным образом вытекает, что это не просто функция. Она всюду определена и сюрьективна и к тому же инъективна, т.е. является взаимно - однозначным отображением или биекцией. Число различных подстановок равно числу перестановок
Pn = n!. В это число входит единичная подстановка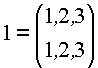 . Зададимся
другой операцией подстановки
. Зададимся
другой операцией подстановки 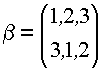 и применим её к ранее полученной конфигурации П2 = (1, 3, 2):
и применим её к ранее полученной конфигурации П2 = (1, 3, 2): 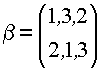 . В результате получилась новая
конфигурация П3 = (2, 3, 1). Следовательно,
композиция подстановок дает новую подстановку g :
. В результате получилась новая
конфигурация П3 = (2, 3, 1). Следовательно,
композиция подстановок дает новую подстановку g :
b
(П2) = b (a (П1)) = g (П1).Назовем бинарную операцию композиции
a
Рис.13.2
Произведя несколько различных операций произведения подстановок, можно убедиться в том, что эта операция ассоциативна. В частности
a ![]() (b
(b ![]() d ) = b
d ) = b
Правда, чтобы окончательно убедиться в этом, нужно проделать слишком много опытов. Ведь здесь имеется шесть различных подстановок, а число составленных из них троек (определяемое как число размещений с повторениями) равно
U63 = 63 = 216.
Проверка коммутативности произведения подстановок дает отрицательный результат: a
Таблица 13.1
1 |
a |
b |
g |
d |
e |
|
1 |
1 |
a |
b |
g |
d |
e |
a |
a |
1 |
g |
b |
e |
d |
b |
b |
d |
e |
a |
g |
1 |
g |
g |
e |
d |
1 |
b |
a |
d |
d |
b |
a |
e |
1 |
g |
e |
e |
g |
1 |
d |
a |
b |
Беспорядком называется подстановка, при которой ни один из элементов конфигурации не остается на своем месте. В рассмотренном примере беспорядков только два: b и e
.Латинским прямоугольником называется конфигурация из
m строк и n столбцов. Каждая строка представляет одну перестановку и, в то же время, каждая строка, кроме первой, задает один беспорядок. Латинский прямоугольник называется нормализованным, когда в первой строке все элементы расположены в естественном порядке. При m = n латинский прямоугольник превращается в латинский квадрат.При
m = 2, n = 3, как в рассмотренном примере с перестановками, существует всего два нормализованных латинских прямоугольника (рис. 13.3).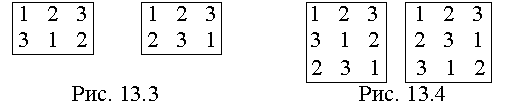
Ненормализованных прямоугольников получается в
n! раз больше, так как верхняя строка может быть задана n! = 6 способами. Нормализованных латинских квадратов при n = 3 имеется также два (рис. 13.4). Они отличаются расположением второй и третьей строк. Заметим, что всегда mПроще всего получать латинские прямоугольники циклическим сдвигом строк, но возможны и другие варианты (рис. 13.5).
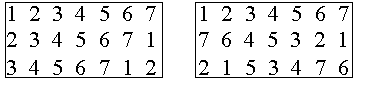
Рис. 13.5
Комбинаторику интересуют не сами латинские прямоугольники, а связанные с ними типовые задачи перечисления. Число латинских прямоугольников, состоящих из одной строки, определяется просто. Оно равно числу перестановок из
n элементов Pn = n! Из них один прямоугольник будет нормализованным, остальные - нет.При
m = 2 число латинских прямоугольников равно числу беспорядков Dn,0, увеличенному в n! раз, так как первая строка может быть задана n! способами. Число Dn,0 мы определим позже (индекс "0" означает отсутствие элементов, оставшихся на своих местах). При m = 3 определение числа латинских прямоугольников представляет сложную задачу, но с уже известным алгоритмом решения. А вот при mНайдем число беспорядков
Dn,0. Подобные задачи решаются методом просеивания конфигураций, т.е. постепенного отбрасывания таких элементов, которые не отвечают определенным требованиям. Применяемый для просеивания метод называют комбинаторным решетом. Для решения поставленной нами задачи используем в качестве решета выведенную в третьем разделе данного курса теоретико-множественную формулу включения и исключения: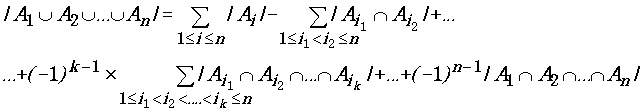
Рассмотрим выделенный промежуточный член, выражающий общую формулу для
k-го члена. Член этот имеет вид суммы, каждое слагаемое которой есть мощность пересечения k множеств. Величины слагаемых зависят от состава пересекаемых множеств и в общем случае неизвестны, но число слагаемых определяется точно, как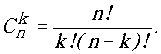
Если множество всех перестановок обозначить М, то это же множество будет являться множеством возможных подстановок, следовательно
|M| = n!
В это число входят как беспорядки, так и подстановки, беспорядками не являющиеся, которые придется отсеять. Определим
W1 М M, как совокупность всех подстановок, у которых первый элемент остается на своем месте, а остальные переставляются произвольно всеми мыслимыми способами. Подстановки, принадлежащие W1, не являются беспорядками. Аналогично определим подмножества: W2, W3,...Wn, у которых соответственно второй, третий, ... элементы остаются на своих местах. Объединение подмножеств W1, W2,... составит множество всех подстановок, не являющихся беспорядками. Число беспорядков выразится разностьюDn,0 = n! - |W1
ИW2И...ИWn|.Величину мощности объединения можно заменить соответствующим рядом членов по формуле включения и исключения, но мы воспользуемся общим выражением промежуточного члена этой формулы. Промежуточный член состоит из С
nk слагаемых, а каждое слагаемое равно числу элементов пересечения k множеств. Элементы пересечения должны одновременно принадлежать всем пересекающимся множествам. Значит, этими элементами окажутся подстановки, у которых на своих местах остаются элементы с индексами i1, i2,...ik. Разнообразие подстановок будет получаться только за счет оставшихся n-k индексов. Это в свою очередь означает, что каждое слагаемое в промежуточном члене равно (n-k)!, а весь промежуточный член равен
Подставляя это общее выражение в формулу числа беспорядков, получим:
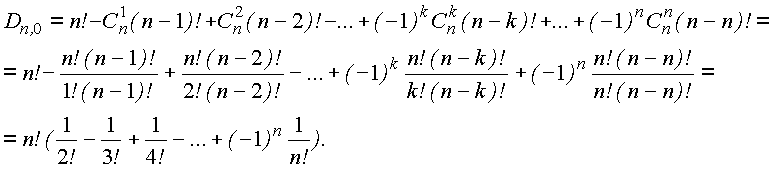
Ряд, находящийся внутри скобок, в математике известен. При бесконечном количестве членов их сумма сходится к 1/е. Следовательно, при больших
n число беспорядков приближенно определяется как Dn,0 @ n!/e.Выведенная нами формула позволяет решить и более сложную и общую задачу о встречах. Конкретная постановка задачи может быть например следующей. Имеется две колоды из
n карт каждая. В первой колоде сохраняется некоторая упорядоченность. Сколькими способами можно уложить вторую колоду так, чтобы затем, при одновременном открывании верхних карт обеих колод, получилось ровно k совпадений?Математически это означает, что нужно найти число подстановок из
n элементов с k совпадениями, т.е. число Dn,k. Искомое число нужно искать как произведение двух сомножителей: числа сочетаний остающихся на месте элементов, т.е. Cnk, и числа беспорядков, образуемых остальными элементами, т.е. D(n-k),0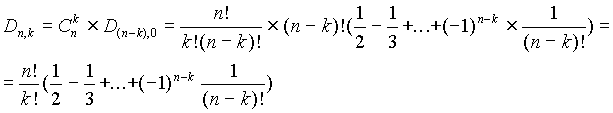
С помощью выведенной нами формулы подобные задачи решаются просто. Например, приняв
n=36 и k=4 получим D36,4 @ 1037.