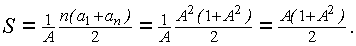
12.
Основы комбинаторики (лекция 12)Комбинаторика изучает комбинаторные конфигурации, т.е. возможные варианты выбора и расположения элементов некоторого, (обычно конечного) множества. При этом комбинаторика интересуется только теми задачами, которые связаны именно с многовариантностью конфигураций.
Рассмотрим в качестве примера "магический квадрат", у которого суммы чисел по строкам, столбцам и диагоналям равны, а сами числа должны составлять натуральный ряд: 1, 2, 3, . . .
A 2, где A - длина стороны квадрата, выраженная числом клеток. Магический квадрат со строной A = 3 показан на рис. 12.1.4 |
9 |
2 |
3 |
5 |
7 |
8 |
1 |
6 |
Рис. 12.1
С этой старинной головоломкой можно связать различные задачи абстрактно-математического характера. Можно, например, заняться поиском формального алгоритма составления магических квадратов, но эта задача будет лишь отчасти комбинаторной. Можно определить в общем виде сумму чисел, которая по определению должна быть постоянной величиной для магического квадрата с заданной стороной А. Числа в клетках образуют арифметическую прогрессию с разностью, равной единице и числом членов, равным А
2. Искомая сумма определится как сумма прогрессии, деленная на А: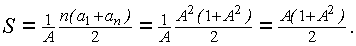
Эта задача тоже имеет лишь косвенное отношение к комбинаторике. Чисто комбинаторной задачей явилось бы определение в общем виде числа возможных магических квадратов при заданном А. Эта задача несравненно труднее двух первых. Если исключить очевидные преобразования магического квадрата путем его поворота на 90о или зеркального отражения, то число действительно разных магических квадратов определить трудно. Перебором возможных конфигураций задачу можно решить для частных случаев при небольших размерах квадрата. Общее решение задачи до сих пор не найдено.
Определение числа возможных конфигураций представляет типичную комбинаторную задачу, так называемую задачу перечисления, причем, получаемые здесь результаты имеют чрезвычайно широкое применение не только в самой комбинаторике, но и практически во всех приложениях дискретной математики. Поэтому мы рассмотрим ряд подобных задач, начиная с простейших.
Мощность декартова произведения множеств определим, исходя из следующих соображений. Согласно определения, декартово произведение
![]()
m
множеств с мощностями соответственно n1, n2, ...nm состоит из кортежей длиной m. На первом месте в каждом таком кортеже стоит один из элементов множества М1, на втором - элемент из М2, и т.д.Для решения поставленной задачи соберем все кортежи с одинаковыми первыми элементами в отдельные классы. Всего таких классов очевидно будет
n1, по числу элементов во множестве M1.. Внутри каждого класса произведем разбиение по второму элементу кортежа. Число таких подклассов (внутри каждого класса) будет равно n2. Действуя далее аналогично, мы дойдем до подклассов самого низшего уровня, в каждом из которых будет только по одному кортежу. В итоге общее количество кортежей, т.е. элементов декартова произведения, составитn = n1? n2? ...? nm
Выведенную нами формулу можно как теорему использовать при решении других аналогичных задач. В комбинаторике эта теорема называется правилом умножения: сперва подсчитывается число конфигураций на первом шаге выбора, затем на втором шаге и т.д., а общее число конфигураций получается перемножением результатов на шагах.
Мощность декартовой степени определяется аналогично
|Mm| = |M|m = nm.
Элементы декартовой степени в комбинаторике имеют специальное название: размещение с повторениями из n элементов по m. Число таких размещений, как мы только что доказали, равно:
Unm = nm
Эта формула дает готовые ответы на вопросы вроде следующих: “Сколько существует различных трехзначных десятичных чисел?”, “Сколько можно придумать четырехбуквенных слов в русском алфавите?”. Решим с ее помощью задачу о числе различных булевых функций от
k аргументов. Ряд значений аргументов булевой функции представляет двоичный цифровой кортеж длиной k. Всего таких кортежей согласно полученной нами формулы будет 2k. Чтобы задать одну функцию, нужно записать ряд её двоичных значений. В этом ряду будет столько цифр, сколько существует кортежей значений аргументов, т.е. тоже 2k. Всего разных функций наберется столько же, сколько существует различных двоичных кортежей длиной 2k, т.е.Размещения без повторений получаются из конфигураций предыдущего вида, если исключить из декартовой степени все кортежи с повторяющимися элементами. Чтобы определить число таких конфигураций, разобьём их множество на классы с одинаковыми первыми элементами. Поскольку число таких элементов равно
n, то и классов будет n. На втором шаге разобъем каждый класс на подклассы по второму элементу. Так как элементы не должны повторяться, а один из них уже стоит на первом месте в кортеже, то подклассов на втором шаге разбиения будет только n - 1. На третьем шаге получим n -2 и т.д. Последний, m - ый элемент можно будет выбрать n - (m - 1) способами, ведь m - 1 элементов уже занято. По этим рассуждениям составляется формула, которую приходится упрощать искусственным способом: .
.
Полученная формула отвечает на вопросы вроде следующего: “Сколькими способами можно подпаять к стандартному 48-контактному разъему 15 проводов (каждый провод к одному контакту)?”
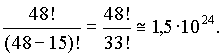
Частный случай размещения без повторений получается при
n = m, т.е. когда число элементов в исходном множестве совпадает с длиной рассматриваемых кортежей. Размещения этого вида называются перестановками, а их число обозначается .
.
Другой вид конфигураций получим, если будем рассматривать не кортежи, а неупорядоченные подмножества. Они называются сочетаниями из
n элементов по m. Число Сnm различных сочетаний из по m определим из следующих соображений. Если бы это были не множества, а кортежи длиной m, то их число равнялось бы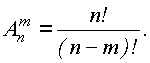
При переходе от кортежей к неупорядоченным множествам
число конфигураций должно уменьшиться. Ведь из всех выборок, отличающихся только порядком перечисления элементов, нужно оставить только одну. А мы уже знаем, что число конфигураций, отличающихся только порядком элементов равно P m = m!. Следовательно, число сочетаний равно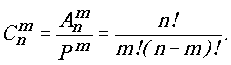
Числа этого вида известны под названием биномиальных коэффициентов, поскольку существует равенство
![]()
Это равенство часто называют "биномом Ньютона", хотя оно было известно задолго до Ньютона и использовалось в частности Паскалем. Паскаль использовал также равенство
![]()
которое доказывается следующим образом:
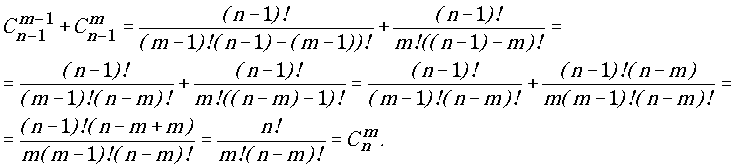
Из доказанного равенства вытекает, что биномиальные коэффициенты можно находить последовательно, один за другим, увеличивая
n и m и суммируя найденные значения. Этот алгоритм наглядно описывается треугольной таблицей, называемой "треугольником Паскаля", в которой n- это номер строки, а m - номер числа в строке (начиная с m=0) Треугольник Паскаля до n = 4 показан на рис. 12.2. каждый элемент треугольника представляет сумму двух ближайших элементов из предыдущей строки.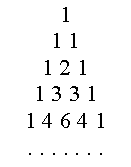
1 4 6 4 1
Рис. 12.2
Рассмотрим ещё один вид конфигураций. Нам уже известно, что разбить заданное множество М на классы можно разными способами. Найдем число
Рассуждения будем строить по правилу умножения. Для составления класса М
1 нужно отобрать m1 элементов исходного множества М. Число вариантов такого выбора равно числу сочетаний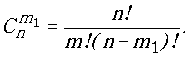
Для составления класса М
2 придется подбирать элементы из числа оставшихся n - m1. Следовательно, число сочетаний в этом случае выразится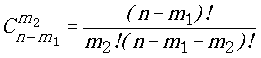
и далее аналогично. Общее число возможных разбиений определится как произведение всего ряда найденных указанным путем чисел
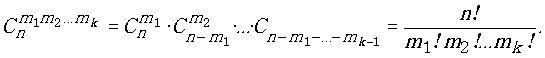
Полученное число является общим видом полиномиального коэффициента и может использоваться для разложения степенных полиномов с числом степеней больше двух. При
k = 2 эта формула превращается в более известную формулу биномиального коэффициента.