11

11. Отношения порядка. Решётки (Лекция 11)

отношение порядка и его свойства,
частично упорядоченное множество,
супремум и инфимум, решетки,
примеры решеток,
многозначная логика и примеры изоморфизма и гомоморфизма,
логика выбора и нечеткие множества

Отношение частичного порядка a b указывает для некоторых, но не обязательно для всех пар (a, b) О А², какой из элементов является предшественником (антецедентом), а какой - последователем (сукцедентом). Оно обобщает известное отношение a < b, которое применимо только к элементам, имеющим количественное содержание.

Если существует a b, то обязательно выполняется и обратное отношение a b. Сейчас нас не так должно интересовать, какой вариант отношения: прямой или обратный имеет место, сколько наличие или отсутствие отношения данного вида между сравниваемыми элементами. Дело в том, что частичный порядок подразумевает возможность существования пар несравнимых элементов.

Будем сравнивать трехразрядные двоичные коды А и В, причем будем считать, что А В, если в каждом разряде кода А цифра меньше или равна цифре соответствующего разряда кода В. Тогда для некоторых пар кодов будет существовать отношение "А - предшественник В", для других пар будет существовать обратное отношение, а в третьих парах элементы окажутся несравнимыми: 010 110; 101 101; 111 101; 000 000; 010 и 100 - несравнимы.

Когда несравнимых пар нет, т. е. отношение a b или a b выполняется для любых пар элементов, отношение частичного порядка превращается в отношение линейного порядка. Иначе говоря, отношение линейного порядка является полностью определенным соответствием

" a " b((a b) U (a b).

Очевидно, отношение линейного порядка является частным случаем отношения частичного порядка. В дальнейшем мы будем использовать термин "частичный порядок" в общем смысле, не подразумевая непременного наличия несравнимых элементов.

Отношение нестрогого порядка рефлексивно, т.е.

" а (а а)

и антисимметрично

" а " b ((a b) & (b a) ® (a = b)),

т.е. из одновременного существования прямого и обратного отношения вытекает равенство а = b, которое следует понимать как тождество, когда а и b - один и тот же элемент.

Антисимметричность представляет особый случай асимметрии, когда симметрия существует, как исключение, только для случая aRa. В матрице смежности такого отношения симметрия наблюдается только для элементов главной диагонали, роль которых исполняют единицы.

Отношение строгого порядка нерефлексивно (никогда не может существовать аRа) и вследствие этого оно уже не может быть антисимметричным, оно просто несимметрично.

Любое отношение порядка транзитивно

" a " b " c((a b) & (b c) ® (a c)).

Примером частичного нестрогого порядка, кроме рассмотренного выше сравнения двоичных кодов, является отношение включения на множестве всех подмножеств некоторого множества А. Если сравниваются подмножества В Н А и С Н А, то отношение В С существует, когда В Н С. Возьмем, например: А = { a, b, c} . Отношение нестрогого включения на будет существовать для пар:

{ a}Н { a} ; { b}Н { a, b}и др.,

обратное отношение будет существовать для пар:

{ b, c} К { b} ; { a, c} К { a, c}и др.,

а также будут иметься несравнимые пары элементов:

{ a} и { b} ; { a, c} и { a, b} и др.

Примером частичного строгого порядка является отношение строгого включения В М С на .

Примерами линейных порядков являются известные отношения "больше" или "меньше" на множестве действительных чисел. При этом различаются отношения нестрогого линейного порядка А В и строгого линейного порядка А < В.

Частично упорядоченным множеством (ЧУМ) называется любое множество, если, по крайней мере, для некоторых пар его элементов установлено отношение порядка. Если отношение порядка установлено для любой пары элементов, множество будет линейно упорядоченным множеством (ЛУМ). Очевидно, ЛУМ есть частный случай ЧУМ. Примером ЧУМ могут быть должности в учреждении: между некоторыми из них установлено отношение подчинения, а другие являются несравнимыми (должности из разных отделов). Примерами ЛУМ являются: множество натуральных чисел, множество действительных чисел и другие множества, построенные на их основе. Все подмножества ЛУМ также являются ЛУМ.

В зависимости от вида отношения порядка, установленного на множестве, само множество получает определения: строго или нестрого упорядоченное ЧУМ или ЛУМ. Чтобы задать ЧУМ нужно определить два объекта: множество А и отношение порядка R. В общем виде получается кортеж

Мы видим, что ЧУМ является моделью, то есть разновидностью математической системы, сигнатура которой состоит только из отношений. При этом ЧУМ является простейшей из моделей, так как использует только одно отношение. Свойства отношения порядка могут быть указаны в названии множества (взамен отдельных аксиом, ввиду немногочисленности и простоты этих свойств), а конкретные связи между элементами придется задавать таблицами или графами. Характерные для алгебр аналитические представления для ЧУМ невозможны, ввиду неоднозначности образа в задаваемых соответствиях.

Сравнительно просто описываются ЛУМ. На рис. 11.1 показаны графы ЛУМ для случаев строгого и нестрогого порядка.

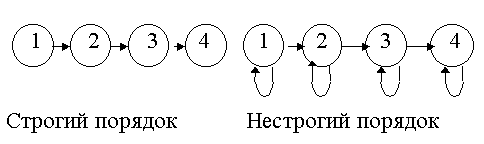
Рис. 11.1

Для ЛУМ графическое или табличное задание не требуется ввиду простоты этой модели. Упорядоченный перечень элементов (кортеж 1, 2, 3, 4) вполне достаточен. Совсем иначе обстоит дело с ЧУМ общего вида (рис. 11.2). Из рисунка видно, что пара (b, c) несравнима. Ясно, что без таблицы или графа такое ЧУМ задать нельзя.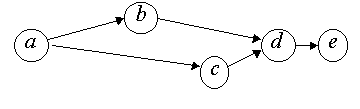

Рис. 11.2

Введем новые понятия, связанные с частично упорядоченными множествами. Возьмем ЧУМ, заданное графом (рис. 11.3). Будем считать отношение порядка на множестве A = { a, b, c, d, e, f, g, h} нестрогим. Петли, характеризующие рефлексивность нестрогого порядка, на рисунке не показаны, но будут подразумеваться. Пользуясь рисунком можно выделить те или иные упорядоченные пары элементов, например, а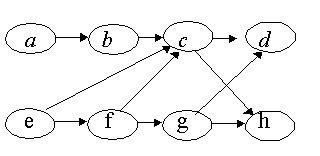 b, и несравнимые пары, например (с, g).

Рис. 11.3

Условимся называть элемент х верхней гранью или максимумом y и z, если y х и z х. Записывать это будем так:

х = Мах { y, z} .

В данном ЧУМ:

c = Max { a, b} ; c = Max { a, c} ; c = Max { c, e} ; d = Max { a, f} .

Hаименьшую верхнюю грань из всех возможных для данной пары элементов будем называть строгим максимумом или супремумом и записывать как

х = sup { y, z} .

В данном ЧУМ супремумами будут, например c = sup { a, e} и h = sup { g, h}. Аналогично определим х как нижнюю грань или минимум у и z , если х у и х z. Записывается это как

х = Min { y, z} .

Наибольшую нижнюю грань будем называть строгим минимумом или инфимумом и обозначать

х = inf { y, z} .

В данном ЧУМ с = inf { c, d} , f = inf { c, g} .

Установив смысл понятий максимума, минимума, супремума и инфимума, расширим их определение на любое подмножество ЧУМ или на всё ЧУМ. В данном примере: d = sup { a, b, c, d, e, f, g} ; c = sup { a, b, e, f} ; e = inf { c, d, e, f,} ; f = inf { c, g} , но a не является инфимумом { b, c} , так как у этой пары есть больший минимум b. У подмножества { b, c, f, g} М A, как и для всего А, нет супремума потому, что для них существует два несравнимых максимума: d и h. У подмножества { b, c, f, g} М A нет не только инфимума, но и ни одного минимума.

Понятия супремума и инфимума широко применяются в современной математике и её приложениях в технических науках. Максимумы и минимумы континуальной математики являются их частными случаями. Они обозначаются max и min, определяются на множестве действительных чисел, т.е. на ЛУМ, и, в отличие от рассмотренных в этой лекции понятий, непременно принадлежат тому подмножеству (отрезку), на котором определяются.

Решеткой (lattice) или структурой называется модель, представляющая ЧУМ с аксиомой: для всех элементов подмножества В М А имеются sup B и inf B. Граф на рис. 11.2 изображает решётку, а ЧУМ на рис. 11.3 не является решеткой. Ещё один пример решётки показан на рис. 11.4, а ЧУМ, не являющегося решёткой - на рис. 11.5.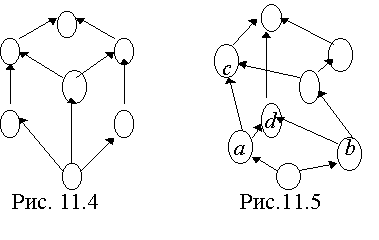

Петли у вершин графов не показаны, но подразумевается рефлексивность отношения (нестрогий порядок). В ЧУМ на рис. 11.5 два несравнимых максимума имеют элементы а и b: Max { a, b} = c и Max { a, b} = d . Кроме того, элементы c и d имеют два несравнимых минимума: Min{ c, d} = a и Min{ c, d}= b.

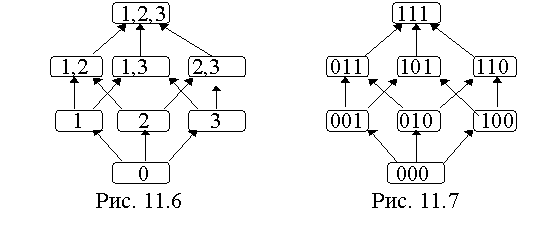
Нетрудно доказать, что булеан с отношением включения образует решётку. В модели имеются несравнимые пары, например { a₁, a ₃}и { a₂}, но всё равно для любой пары элементов определены супремум и инфимум. В частности sup { { a₁,a₃}, { a₂} } = { a₁, a₂, a_3}и inf { { a₁, a₃} ,{ a₂}}= Ж. Взяв конкретное значение n = 3 и заменив Ж = 0; а₁ = 1; а₂ = 2; а₃ = 3 построим решетку (рис. 11.6).

Аналогичную решётку образует множество полиномов над GF(2²) с отношением частичного порядка. Заменяя полиномы от фиктивной переменой х двоичными цифровыми кодами, получим решетку (рис. 11.7).

Графы решеток, как правило, изображаются упрощенно, без дуг, показывающих транзитивные замыкания путей, и без петель, указывающих на рефлексивность отношения нестрогого порядка. Напомним, что порождающее решётку отношение непременно должно быть рефлексивным, иначе не для всех пар элементов найдутся sup и inf.

В последней решетке (рис. 11.7) обнаруживается сходство с совсем другой моделью - единичным кубом, который является неориентированным графом. На единичном кубе тоже можно установить некоторые виды отношений, но ими могут быть только симметричные отношения: например отношение "быть соседом" или "иметь кодовое расстояние, равное единице " для двух кодов. Это отношение нерефлексивно и нетранзитивно.

В заключение обзора отношений приведем классификационную таблицу (табл. 11.1)

Таблица 11.1

Рефлексивные	Симметричные	Транзитивные А = В
		Нетранзитивные “А противоречит В”
	Антисимметричные	Транзитивные “А делит В”
		Нетранзитивные “А – врач В”
Нерефлексивные	Симметричные	Транзитивные “А соединено с В”
		Нетранзитивные “А встречается с В”
	Несимметричные	A < B
		А Ю В

Продолжим знакомство с фактами внешнего сходства математических систем и настоящего изоморфизма. Вернемся к булеану. Будем теперь считать его носителем алгебры с теоретико-множественными операциями E , C и ` x . Примем самое простое множество М = { a, b} и исследуем алгебру

Составим для этой алгебры таблицы Кэли (табл. 11.2, 11.3 и 11.4) и исследуем их.

Таблица 11.2

И	Ж	{a}	{b}	{a,b}
Ж	Ж	{a}	{b}	{a,b}
{a}	{a}	{a}	{a,b}	{a,b}
{b}	{b}	{a,b}	{b}	{a,b}
{a,b}	{a,b}	{a,b}	{a,b}	{a,b}

Таблица 11.3

З	Ж	{a}	{b}	{a,b}
Ж	Ж	Ж	Ж	Ж
{a}	Ж	{a}	Ж	{a}
{b}	Ж	Ж	{b}	{b}
{a,b}	Ж	{a}	{b}	{a,b}

Таблица 11.4

х	Ж	{a}	{b}	{a,b}
` х	{a,b}	{a,b}	{a}	Ж

Свойства этой алгебры своеобразны: здесь нет группы по операции И, так как нет противоположного элемента, нет группы по З, так как нет обратного элемента, хотя есть элемент, выполняющий роль единицы: { a,b} . Как уже раньше было доказано, булеан образует решетку.Таким образом, булеан оказался носителем двух совершенно разных систем: алгебры подмножеств ; И, З, ` х и модели типа решетки ; Н . Это оказалось возможным ввиду совпадения по содержанию операций И и З с одной стороны и взятия супремума и инфимума на булеане - с другой.

Рассмотрим ещё одну математическую систему, которая полностью изоморфна алгебре подмножеств, - многозначную логику.

Примем три категории истинности:

х = 0, когда "х" ложно,

х = а, когда "х" истинно в смысле "а",

х = b, когда "х" истинно в смысле "b",
х = 1, когда "х" истинно в любом смысле.

Введем операции Ъ, & и ` х, свойства которых зададим с помощью таблиц Кэли (табл. 11.5, 11.6 и 11.7)

Таблица 11.5

Ъ	0	a	b	1
0	0	a	b	1
a	a	a	1	1
b	b	1	b	1
1	1	1	1	1

Таблица 11.6

&	a	b	1
0	0	0	0
a	a	0	a
b	0	b	b
1	a	b	1

Таблица 11.7

x	0	a	b	1
`x	1	b	a	0

Если мы определим отношение частичного порядка R таким образом, что 0 < а; 0 < b; a < 1 и b < 1, то множество принятых значений переменной "х" образует решётку. От трехзначной (фактически - четырехзначной) логики можно перейти к четырехзначной (фактически - восьмизначной) логике и т.п. Все эти логики могут быть представлены как решётки.

Логика выбора (непрерывная логика) среди многозначных логик занимает особое место. Число значений переменной "х" здесь принципиально бесконечно. Сама переменная "х" представляет точку на действительной числовой оси, а множество её значениё образует ЛУМ. Любое подмножество М имеет как max, так и min. Верхнюю точку ЛУМ М (наибольшее число) обозначим p = max M, а нижнюю- (наименьшее число) - q = min M. Центром множества назовем величину 0,5(p+q). Ясно, что точки p и q по отношению к центру расположатся симметрично. Инверсией х назовем точку, расположенную симметрично "х" относительно центра (рис. 11.8). Инверсию можно выразить так:

0,5(х + `х) = 0,5(p + q); откуда ` х = p + q - х.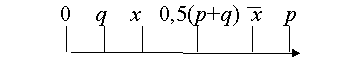

Рис. 11.9

Логика выбора является алгеброй вида М; max, min, ` х, где М -бесконечное ЛУМ, хотя все практически используемые числа от р до q могут быть конечными.

Операции max и min ассоциативны и коммутатвны, а также дистрибутивны одна отосительно другой, аналогично операциям булевой алгебры.

max(min(a,b), min(a,c)) = min(a, max(b,c)) аналогично abЪ ac = a(bUЪc);

min(max(a,b), max(a,c)) = max(a, min(b,c)) аналогично (aЪ b)(bЪ c) = aUЪbc.

Cвойство де-Моргана:

Идемпотентность: max(x,x) = x; min(x,x) = x;

Инволюция: = х;

Нейтральность граней: max(x,q)=x; min(x,p) = x аналогично xU 0 = х; x1=x;

Экстремальность граней: max(x,p)=p; min(x,q)=q аналогично xU 1=1; x0=0.

Перечисленные свойства сближают логику выбора с булевой алгеброй. Но есть свойства, которые немыслимы в булевой алгебре. Операции логики выбора довольно просто сочетаются с обычными алгебраическими операциями, с которыми они дистрибутивны:

a * max (b, c) = max (a * b, a * c);

a + max (b, c) = max (a + b, a + c);

max (a, b) + ma x(c, d) = max (a + c, a + d, b + c, b + d);

Аалогичные равенства существуют и для min. Кроме того, в логике выбора используется операция выделения модуля |x|. Её применяют для получения значений min и max.

max (a, b) = 0,5(a+b+|a-b|);

min (a, b) = 0,5(а+b - |a-b|).

Логика выбора шире булевой алгебры и перекрывает её. Иначе говоря, логика выбора гомоморфна булевой алгебре. Логика выбора уже десятки лет используется теорией обработки аналоговых (непрерывных) сигналов.

С недавних пор получила известность ещё одна система, очень близкая логике выбора и в основной редакции изоморфная ей. Это - теория нечетких множеств. Здесь используется понятие "лингвистической переменной" m, которая может принимать не только числовые, но и некоторые условные значения: "интересный", "тёмный" и т.п. Во всяком случае, эти значения могут быть выражены с помощью отношения частичного порядка и могут образовывать модели типа решётки. В современной теории нечетких множеств для выражения относительных значений лингвистической переменной применяют специальную функцию f(m) = 0 при mПM и f(m) = 1 при mОM. Для промежуточных значений функции f(m) используется специальная величина m (0 m 1). Она является количественной характеристикой, выражающей степень уверенности в принадлежности mОM. Для переменной m действительны все описанные выше операции логики выбора.

Содержание