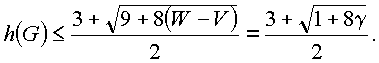
9.
Неориентированные графы (лекция 9)Граф - это геометрический образ бинарного отношения. Если отношение определяется на множестве А
= { a, b, c, d, ...} , то элементы этого множества изображаются точками (кружками), которые называются вершинами графа и имеют соответствующие обозначения a, b, .... Те элементы, для которых существует отношение R, например отношение эквивалентности, соединяются линиями, которые называются ребрами. Очевидно, таким рисунком можно описать любое симметричное отношение на конечном множестве, т.е. такое R, для которого из aRb вытекает bRa. При несимметричности отношения ребра следовало бы снабжать стрелками, указывающими, какое именно отношение имеет место - прямое или обратное. Сам граф в этом случае получает название ориентированного графа. В данной лекции будут рассмотрены только неориентированные графы.Длина и форма ребер графа не имеют значения. Безразлично и взаимное расположение вершин на плоскости, хотя практически выбирают их расположение так, чтобы свести к минимуму число пересекающихся ребер. Если граф может быть вычерчен без пересечения ребер, он называется планарным
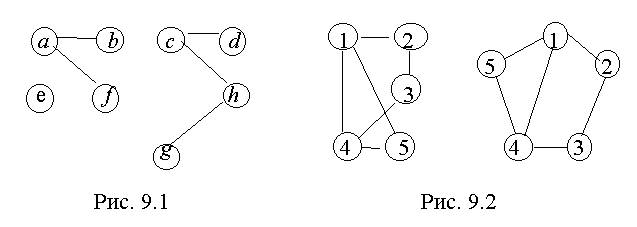
.Различают графы связные, у которых все вершины соединены между собой последовательностью ребер, и несвязные, у которых это условие нарушено. На рис. 9.1 показан несвязный граф, а на рис. 9.2 - два равносильных изображения одного и того же связного графа.

В некоторых приложениях теории графов встречаются графы с кратными ребрами. Такие графы называются мультиграфами (рис.9.3).
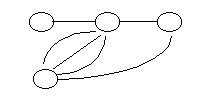
Рис. 9.3
Графы считаются изоморфными если их можно получить один из другого путем переименования вершин. Возможность произвольно менять расположение вершин при их большом числе может вызвать неудобства для сравнения графов. Поэтому (да и по другим причинам) граф может быть заменен таблицей, описывающей данное отношение. Для графа, показанного на рис. 9.2, получается таблица 9.1.
Таблица 9.1
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
0 |
0 |
3 |
0 |
1 |
0 |
1 |
0 |
4 |
1 |
0 |
1 |
0 |
1 |
5 |
1 |
0 |
0 |
1 |
0 |
Такая таблица называется таблицей смежности. Если исключить заголовки строк и столбцов, таблица превращается в матрицу смежности. При матричном представлении предполагается естественный порядок перечисления вершин. У неориентированных графов матрица смежности всегда симметрична относительно главной диагонали.
В ряде приложений граф нужно описывать более подробно, давая обозначения не только вершинам, но и ребрам. При этом граф задает соответствие, называемое инциденцией, между элементами двух множеств: вершин и ребер. Допустим, что имеется граф с множеством вершин А
= { a, b, c, d, e} и множеством пронумерованных ребер В = { 1,2,3,4,5,6} (рис. 9.4). Составим таблицу инциденций (табл. 9.2).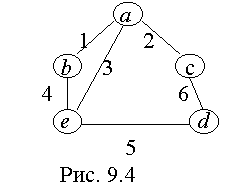
Таблица 9.2
| a | b | c | d | e | |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 1 | 1 |
| 6 | 0 | 0 | 1 | 1 | 0 |
Введем ряд определений. Степенью
deg ai вершины ai называется число ребер, инцидентных данной вершине. Оно равно числу единиц в соответствующем столбце таблицы или матрицы инциденций. Поскольку каждое ребро имеет два конца, тоa deg a = 2W,
где
W - число ребер графа. Отсюда следует, что в любом графе число вершин с нечетными степенями чётно.Регулярным или однородным графом, называется граф, все вершины которого имеют одинаковые степени. Полным называется граф, у которого все вершины соединены попарно ребрами. В этом случае все недиагональные элементы матрицы смежности равны единице.
Если из некоторого графа
G удалить часть вершин вместе с инцидентными им ребрами, то получится подграф H(G). Если же удалить часть ребер, не трогая вершин, то оставшееся множество ребер, тоже считаемое частью графа, называется суграфом S(G). Удалив все ребра, получим нулевой суграф. Говорят, что суграф S(G) покрывает вершины графа G, если любая вершина графа G инцидентна хотя бы одному ребру S(G). Пример графа и покрывающего его суграфа показан на рис. 9.5.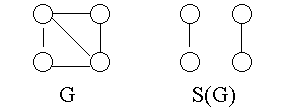
Рис. 9.5
Чтобы сформулировать еще несколько определений, представим путешественника, двигающегося по ребрам графа и проходящего их последовательно одно за другим
Маршрутом M
(G) называется последовательность ребер графа G, имеющих общие инцидентные вершины. В маршруте имеется первое ребро и, если он конечный - последнее. Одно и то же ребро может встречаться в маршруте несколько раз (рис. 9.6).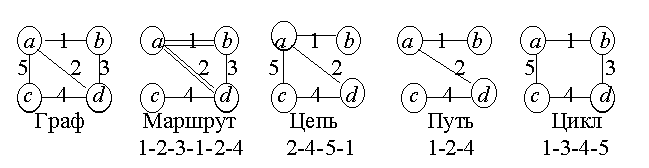
Рис. 9.6
Число ребер в маршруте называется его длиной. Длина маршрута на рис. 9.6 равна 6. Началом и концом маршрута называются вершины, инцидентные его первому и последнему ребру, но не инцидентные второму и предпоследнему (обратите внимание на формальность определения!). Если начало совпадает с концом, маршрут называется циклическим
.Цепь - это маршрут, в котором ребра проходятся не более одного раза. Путь - это цепь, в которой любая вершина инцидентна не более, чем двум ребрам. Любая часть пути тоже является путем. Цикл - это путь, у которого начало и конец совпадают. Для цикла неважно, какую из вершин считать начальной. Примеры всех названных частей графа показаны на рис. 9.6.
Расстоянием d
(a, b) на графе называется минимальная длина пути от вершины а к вершине b. Две вершины, для которых d = 1, называются соседними или смежными.Рассмотрим связный граф, имеющий несколько циклов (рис. 9.7). Удалим некоторые ребра таким образом, чтобы разорвались все циклы, но связность графа не нарушилась. Полученный таким путем суграф без циклов, покрывающий все вершины исходного графа, называется максимальным деревом
T(G). Заметим, что просто деревом T можно называть любой связный граф без циклов, а несвязный граф без циклов иногда называют лесом.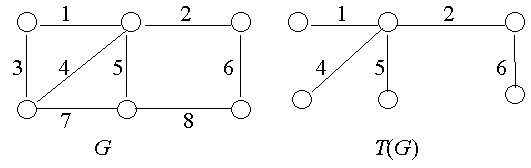
Рис. 9.7
Всего мы удалили три ребра: 3, 7 и 8 . Число удаленных ребер равно числу циклов, первоначально имевшихся в
G. Это число называется цикломатическим числом g (G), а удаляемые ребра называются хордами. Число ребер WT в максимальном дереве на единицу меньше числа вершин дерева и графа VT = VG. Отсюда определяется цикломатическое число:g (G) = WG - WT = WG - VG + 1.
По этой формуле можно найти цикломатическое число, не вычерчивая графа, а имея только матрицу смежности или матрицу инциденций. Совокупность хорд называется дополнением максимального дерева.
Для одного графа может быть получено несколько разных максимальных деревьев. Если ребра в каком-то смысле неравноценны, возникает задача наилучшего выбора максимального дерева или так называемая задача минимального соединения.
Задается граф со взвешенными ребрами, т.е. каждому ребру должно быть присвоено некоторое число, называемое весом или ценой ребра. Требуется найти максимальное дерево с минимальной суммой весов. Задача имеет простой алгоритм решения. Сперва выбирается ребро, имеющее минимальный вес. Если таких ребер несколько, выбор между ними делается случайным образом. Выбранное ребро является первичным деревом. Далее к постепенно разрастающемуся дереву прибавляются новые ребра. Прибавляемое ребро обязательно должно иметь с деревом одну инцидентную вершину, но не две (присоединяемое ребро должно обеспечивать связность дерева, но не образовывать циклов). Из ребер, удовлетворяющих указанному требованию, выбирается ребро с наименьшим весом. Пример решения показан на рис. 9.8. Веса обозначены цифрами, а буквы указывают последовательность присоединения ребер. Штрихами показаны хорды.
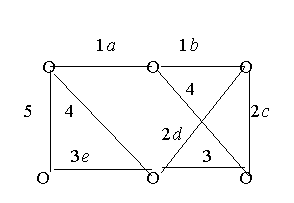
Рис. 9.8
Поиск кратчайшего пути - другая простая задача на неориентированном графе. Задается граф со взвешенными ребрами (например: километраж на дорожной схеме). Задаются две вершины: начальная а0 и конечная ак. Требуется найти путь из начальной вершины в конечную с минимальной суммой весов. Решение состоит в следующем. Вводится мера удаленности L от конечной вершины. Затем, двигаясь от конечной вершины, для которой L = 0, в сторону начальной вершины просматривают все ребра, присваивая инцидентным им вершинам соответствующие нарастающие величины L, которые суммируются по всем пройденным ребрам. Если в вершине сливается два или несколько путей, то выбирается путь с минимальной величиной L и это значение суммы присваивается данной вершине. Окончательный выбор пути происходит только после последнего слияния возможных путей.Хроматическим числом
h(G) графа G называется минимальное число красок, необходимое для того, чтобы любые смежные вершины имели разные цвета. Для определения хроматического числа пользуются приближенными оценками:![]() ;
;