8. Булева алгебра (лекция 8)
Булевой алгеброй в узком смысле называется множество
{0, 1} с двумя бинарными и одной унарной операцией![]()
Дизъюнкция
Ъ (операция "ИЛИ") иногда называется логическим сложением, что неверно, так как она мало похожа на обычное сложение. Поэтому не следует заменять знак дизъюнкции на знак “плюс”. Дизъюнкция двух и большего числа аргументов обращается в нуль только в том случае, когда все аргументы имеют значение нуль. В противном случае она равна единице.Конъюнкция & (операция "И") часто называется логическим умножением и в самом деле очень похожа на умножение. Поэтому знак & часто заменяют точкой или просто опускают. Конъюнкция обращается в единицу только, если все аргументы равны единице.
Инверсия
` х (операция "НЕ х") выполняется одновременно над всем выражением, записанным под чертой, как унарная операция.Свойства операций булевой алгебры, как и любой конечной алгебры, можно выразить с помощью таблиц Кэли (табл. 8.1, 8.2, 8.3). Ввиду связи булевой алгебры с математической логикой, о чем будет сказано дальше, эти таблицы издавна принято называть таблицами истинности. Для удобства пользования такими таблицами в них включают переменную х и инверсию
` х.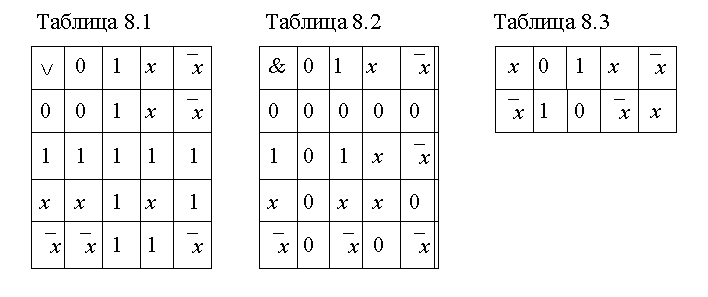
Для операций булевой алгебры действительны некоторые аксиомы, знакомые нам по другим алгебрам:
А
1 : ассоциативность дизьюнкции и конъюнкцииa
Ъ (bЪ c) = (aЪ b)Ъ c; a(bc) = (ab)c;А
2 : коммутативность дизъюнкции и конъюнкцииa
Ъ b = bЪ a; ab = ba;А
3 : существование нейтральных элементов для дизъюнкции и конъюнкцииa
Ъ 0 = 0Ъ a = a; a&1 = 1& a = a;А
5 : дистрибутивность конъюнкции относительно дизъюнкцииa(b
Ъ c) = abЪ ac.Кроме того, в булевой алгебре действуют специальные аксиомы, которых не было в рассмотренных нами примерах алгебр:
А
6 : закон исключенного третьего (вместо аксиомы о существовании противоположного элемента) а Ъ `а = 1;А
7 : закон противоречия (вместо аксиомы о существовании обратного элемента) а &`а = 0;А
8 : дистрибутивность дизьюнкции относительно конъюнкцииа
Ъ bc = (aЪ b)(aЪ c);А
9 : замкнутость множества { 0, 1} относительно инверсии: `0 = 1; `1 = 0.Исходя из этих аксиом, можно вывести как теоремы некоторые удобные для практического применения правила. Для примера докажем правило: х
&0 = 0 (конъюнкция любой переменной с нулем равна нулю). Запишем левую часть доказываемого правила: х & 0 = ... ; ввиду нейтральности 0 для дизъюнкции перепишем так: х & 0 Ъ 0=…; согласно закона противоречия заменим нуль: х & 0 Ъ х & `х=… Ввиду дистрибутивности конъюнкции относительно дизъюнкции вынесем переменную х за скобки: ... = х ( х Ъ 0) = ... ; далее, ввиду нейтральности нуля для дизъюнкции, преобразуем к виду: ... = х & `х = ... ; наконец, вследствие закона противоречия получим: ... = 0. Примерно таким же путем можно доказать и другие правила, применяемые при практической работе с булевой алгеброй:-идемпотентность дизъюнкции и конъюнкции
а
Ъ а = а; а & а = а;-правило поглощения
а
Ъ ab = a; a(aЪ b) = a;-
правило склеиванияab
Ъ a` b = a; (aЪ b)(aЪ ` b) = a;-правило де-Моргана, которое выражает двойственную связь между дизъюнкцией и конъюнкцией
![]()
Булева алгебра самым тесным образом связана с основами теории множеств. Достаточно сузить множество до двух элементов: 0 и 1, как теоретико-множественные операции превращаются в операции булевой алгебры. Объединение становится равносильным дизъюнкции, пересечение - конъюнкции, а инверсия - дополнению.
С другой стороны, булева алгебра связана, во всяком случае, исторически, с логикой. Логика - древняя наука, рассматривающая категории истинности, выводимые путем рассуждений из некоторых известных предпосылок. Классическая логика двузначна, она признает только две категории: истиннно (1) или
ложно (0). В своем развитии она часто наталкивалась на противоречия, которые не удавалось разрешить путем рассуждений. Подобные противоречия назывались парадоксами. Например: "Некто заявляет, что он лжет. Если он при этом говорит правду, то выходит, что он солгал. Если же он действительно лжет, то выходит, что он сказал правду". Логика научилась избавляться от парадоксов только после создания специального формального аппарата, называемого исчислением высказываний. Это стало возможным лишь после изобретения булевой алгебры (Джордж Буль 1848 г.).Булевой алгеброй в широком смысле или алгеброй логики называют множество {0, 1} с любыми сигнатурами, способными заменить сигнатуру (Ъ , &, ` х ). В частности это: исчисление Гильберта с сигнатурой (® , ` х ), алгебра Жегалкина с операциями (Е , &, 0, 1) и др. Операция а ® b (импликация) равна нулю только в том случае, если а = 1, b = 0. Она выражает рассуждение: "Если а - истинно, то должно быть истинно и b", или : "Истинность а влечет истинность b". Равенство нулю результата операции а ® b означает ошибочность этого рассуждения при а = 1 и b = 0.
Алгебра логики со всеми возможными в ней функциями изучается и используется в качестве математической основы в курсе информатики. Поэтому здесь мы ограничимся некоторыми замечаниями общего характера.
В булевой алгебре, как и в любой другой, одну и ту же функцию можно выразить многими способами, используя различные композиции функций, принятых в качестве операций или "связок". В то же время имеется предпочтительная форма выражения, к которой стараются свести функцию, первоначально заданную произвольной формулой или таблицей истинности. В булевой алгебре (в узком смысле) такой предпочтительной формой является дизъюнктивная нормальная форма (ДНФ). Различают просто ДНФ и совершенную ДНФ (СДНФ), имеющую вид
f(a,b,c,d) = abc
` d Ъ a` b` cd Ъ abcd.В каждом члене СДНФ присутствуют символы всех аргументов функции, некоторые из них могут быть с инверсией. Такие члены называются конституентами единицы, так как каждому из них соответствует одна единица в таблице истинности функции.
СДНФ может быть упрощена до минимальной ДНФ, представляющей интерес для последующей аппаратной реализации. Минимальная ДНФ, равносильная первоначальному представлению функции, тоже состоит из элементарных конъюнкций, соединенных знаком
Ъ , но теперь такие члены содержат наименьшее возможное количество букв, да и число членов тоже минимально.Заметим, что применяемые в булевой алгебре равенства имеют мало общего с равенствами, используемыми в обычной алгебре. В обычной алгебре они обычно выражают уравнения. Например, мы приравниваем двучлен
bx + c нулю, а затем отыскиваем корень уравнения bx + с = 0, т.е. такое значение переменной х, которое превращает уравнение в тождество. Можно сказать, что, составляя уравнение, мы тем самым неявно задаем х. Неявное задание функций типично для обычной алгебры. Уравнениеx2/a2 + y2/b2 + z2/c2 = 1
позволяет считать любую из шести переменных функцией пяти остальных, и методы обычной алгебры дают возможность аналитического выражения подобных функций.
В булевой алгебре это невозможно. Нельзя, например, разрешить равенство (а Ъ b)& c = 1 относительно переменной а. Из данного выражения вытекает только, что с = 1 и, кроме того, либо а, либо b равно единице, либо и то и другое вместе.
Равенства булевой алгебры - это только тождества, здесь не может быть уравнений. Для дизъюнкции нет противоположного элемента, а для конъюнкции - обратного, поэтому аргументы нельзя "переносить" из левой части равенства в правую, или наоборот, как это делают в обычной алгебре. В булевой алгебре нельзя присоединять "по ИЛИ" переменную или единицу к обеим частям равенства:
a
Ъ b = c; (aЪ b) Ъ 1 = c Ъ 1; 1 = 1.Для выяснения причины столь сильных отличий от обычной алгебры желательно выяснить принадлежность булевой алгебры (в широком смысле) к одному из видов универсальных алгебр. Определить её как кольцо мешает отсутствие противоположного элемента для дизъюнкции (если считать её аддитивной операцией). Кроме того, неясно, что делать с унарной инверсией. Напрашивается вопрос: нельзя ли заменить дизъюнкцию и инверсию какой-нибудь двухместной операцией, более похожей на сложение? Исходя из таблицы истинности для дизъюнкции, заменим:
0
Ъ 0 = 0 на 0 Е 0Е 0& 0 = 0,0
Ъ 1 = 1 на 0 Е 1Е 0&1 = 1,1
Ъ 0 = 1 на 1Е 0Е 1&0 = 1,1
Ъ 1 = 1 на 1Е 1Е 1&1 = 1.В общем виде: a
Ъ b = a Е b Е a & b; ` x = x Е 1.Таблица 8.4
| Е | 0 | 1 | х | хЕ 1 |
| 0 | 0 | 1 | х | хЕ 1 |
| 1 | 1 | 0 | хЕ 1 | х |
| х | х | хЕ 1 | 0 | 1 |
| хЕ 1 | хЕ 1 | х | 1 | 0 |
Таблица 8.5
| & | 0 | 1 | х | хЕ 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | х | хЕ 1 |
| х | 0 | х | х | 0 |
| хЕ 1 | 0 | хЕ 1 | 0 | хЕ 1 |
Таблицы Кэли (табл. 8.4 и 8.5) для операций Е и & после проделанной замены показывают наличие коммутативной аддитивной группы и мультипликативной полугруппы с единицей. Итак, булева алгебра (в широком смысле) оказалась коммутативным кольцом с единицей, тогда, как алгебра действительных чисел является полем. Именно отсутствие обратного элемента для мультипликативной операции делает булеву алгебру столь непохожей на обычную.