7.Универсальные алгебры с двумя бинарными операциями

(лекция 7)

Кольцом называется алгебра

,

в которой для сложения действительны все аксиомы абелевой группы, для умножения достаточно только аксиомы ассоциативности А1 и установлена специальная аксиома дистрибутивности умножения относительно сложения А5:

Можно сказать, что кольцо представляет соединение абелевой группы по сложению (так называемой аддитивной группы кольца) с мультипликативной полугруппой общего вида. Задавая дополнительно аксиомы о свойствах умножения, можно получить коммутативное кольцо. кольцо с единицей и т.п.

Телом называется кольцо, у которого все отличные от нуля элементы образуют группу общего вида (не обязательно коммутативную). Особое положение нуля в этом определении объясняется тем, что не может быть одного и того же нейтрального элемента для двух операций кольца. Поэтому присутствие нуля в мультипликативной группе неизбежно приводит к противоречию: здесь он не может быть нейтральным элементом, а использование его в качестве одного из обычных элементов противоречит его роли в сложении. В итоге нуль получает уникальные свойства: умножать на него можно, но делить уже нельзя, так как нуль не имеет обратного элемента.

Полем называется тело с коммутативным умножением. Поле представляет соединение двух абелевых групп: аддитивной и мультипликативной, причем нуль имеет те же уникальные свойства, что в кольце или теле.

Перейдем к описанию примеров конечных колец и полей постепенно усложняя аксиоматику умножения. Для сложения, как уже было установлено, необходимы все четыре аксиомы аддитивной абелевой группы: А1 (ассоциативность), А2 (коммутативность), А3 (наличие нуля) и А4 (наличие противоположного элемента).

Пример 1. Рассмотрим алгебру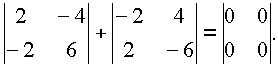 , где носитель образован из квадратных матриц размера , элементами которых являются положительные и отрицательные чётные числа. Сложение матриц ассоциативно и коммутативно. Существует нейтральный для сложения элемент (нулевая матрица). Для каждой из матриц можно подобрать противоположную, например

.

Следовательно, аддитивная группа имеется. Нейтральный элемент для умножения отсутствует, так как для построения единичной матрицы

,

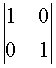требуется нечетное число 1, отсутствующее по определению данной алгебры. Если нет нейтрального элемента, не может быть и обратного. Кроме того, умножение матриц, вообще говоря, не коммутативно:

, но .

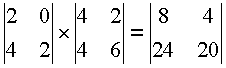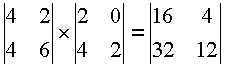Следовательно, в данном примере мы получили кольцо общего вида.

Пример 2. Берем такое же множество матриц, но теперь элементами матриц будут целые числа, положительные и отрицательные. Теперь для умножения будет иметься нейтральный элемент: единичная матрица, которая является и левой и правой единицей мультипликативной полугруппы кольца. Обратные элементы могут иногда найтись, например:

,

но в общем случае их существование не гарантировано. Это можно доказать так. Возьмем равенство

,

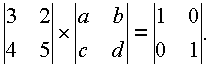в котором первый сомножитель выбран произвольно, а во втором элементы имеют буквенные обозначения. Чтобы узнать, существует ли такое равенство при целых значениях всех чисел, составим и решим систему уравнений, вытекающую из данного равенства.

Равенство удовлетворяется только при дробном значении с. Следовательно, аксиома о существовании обратного элемента здесь не имеет места. Кроме того, умножение остается некоммутативным, вследствие чего в этом примере получается тело.

Пример 3. Возьмем множество чисел М = {0, 1, 2, 3} и определим на нем операции и , т.е. сложение и умножение по модулю 4. Составим таблицы Кэли для обеих операций (таблицы 7.1 и 7.2).

Таблица 7.1

0 1 2 3
0 0 1 2 3
1 1 2 3 0
2 2 3 0 1
3 3 0 1 2

Таблица 7.2

 

0 1 2 3
0 0 0 0 0
1 0 1 2 3
2 0 2 0 2
3 0 3 2 1

Таблица 7.1 показывает все необходимые для аддитивной группы свойства: ассоциативность и коммутативность операции, наличие нуля и противоположного элемента. Последнее видно из наличия нуля в каждой строке. Таблица 7.2 показывает все свойства умножения, кроме наличия обратного элемента. Таким образом, в этом примере получилось коммутативное кольцо с единицей.

Пример 4. Построим алгебру, аналогичную предыдущей, но сложение и умножение теперь будем выполнять по модулю 5. Построим таблицы Кэли (табл. 7.3 и 7.4).

Таблица 7.3

0 1 2 3 4
0 0 1 2 3 4
1 1 2 3 4 0
2 2 3 4 0 1
3 3 4 0 1 2
4 4 0 1 2 3

Таблица 7.4

0 1 2 3 4
0 0 0 0 0 0
1 0 1 2 3 4
2 0 2 4 1 3
3 0 3 1 4 2
4 0 4 3 2 1

Таблица сложения показывает наличие аддитивной коммутативной группы. Таблица умножения показывает ассоциативность и коммутативность операции. Кроме того, в каждой строке или столбце содержится единица, что указывает на аксиомы о существовании единицы и обратного элемента. В данном примере мы получили поле.

Конечные числовые поля вроде полученного в примере 4 называются полями Галуа по имени Эвариста Галуа, который их впервые описал, и который ввёл термины "группа", "поле" и т.п.

Интересна биография Э.Галуа. Обычно знаменитый ученый, оставляющий глубокий след в истории науки, достигает этого в итоге большого трудового жизненного пути. Наследие такого ученого бывает великим не только по своему значению, но и просто по объему материала. И. Ньютон прожил 85 лет, А.Н. Крылов - 82, Леонард Эйлер -76 ( да еще имел 13 детей от двух жен!), Галилео Галилей - 78, Н.Е. Жуковский -74. Бывают и короткие биографии, но насыщенные плодотворным трудом, как у Блеза Паскаля, который прожил всего 39 лет и из них последние девять - в монастыре, в болезненном состоянии, когда он уже не работал. Но за предшествующие одиннадцать лет он создал гидростатику, заложил основы комбинаторного анализа, построил первые вычислительные машины и другие замечательные механизмы. Иначе сложилась судьба Галуа. Вся его теоретическая работа уместилась на нескольких страницах письма, написанного им в ночь перед дуэлью, на которой он был убит в возрасте 21 года (в 1832 г). Ранее он дважды подавал свои записки во французскую Академию, но оба раза маститые академики Коши и Фурье теряли рукопись, не поняв её значения.

Для обозначения в общем виде числовых полей Галуа принята запись GF(p), где р - простое число, являющееся модулем пересчета при сложении и умножении. При составном р получается не поле, а кольцо G(p), как в нашем третьем примере. Поля и кольца Галуа иначе называются просто полями или кольцами вычетов по модулю р. Самым простым из таких полей является GF(2), описываемое таблицами 7.5 и 7.6. Оно играет важную роль в теории    кодирования цифровой информации, с его помощью образуются более сложные алгебраические системы.

Таблица 7.5

0 1
0 0 1
1 1 0

Таблица 7.6

0 1
0 0 0
1 0 1

Кольцо полиномов GF(pk) является расширением понятия поля вычетов по модулю простого числа р. Здесь элементами поля являются не числа, а полиномы (многочлены) k - ой степени от фиктивной переменной х, имеющие вид:

где коэффициенты а GF(p) = { 0, 1, ..., p -1} . Переменной x можно не придавать особого смысла. Она введена для образования степеней, делающих возможным непосредственное сложение (приведение по модулю р) только членов одинаковой степени. Знак (умножение по модулю р) для упрощения записи опускается.

Полиномы можно складывать и умножать, соблюдая правила действий по модулю р. Примеры при р = 5: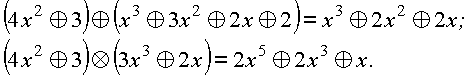

Как и при умножении полиномов обычной алгебры, степени перемножаемых членов складываются. Полиномы над GF(p) можно делить с остатком или нацело, если определить для коэффициентов операцию вычитания по модулю р. Пример деления без остатка при р = 5:

Проще всего операции с полиномами выполняются при р = 2, так как операции сложения и вычитания по модулю 2 дают одинаковый результат, и вводить отдельную операцию вычитания не нужно. Кроме того, умножение на множестве {0, 1} очень просто. Знак умножения и коэффициенты 0 и 1 не пишутся.

Примеры операций с полиномами над полем GF(2). Умножение:

;

Деление с остатком:

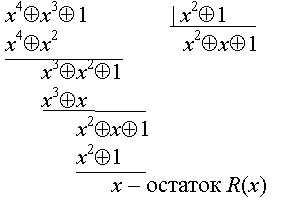
Приведенные здесь примеры дают представление о полиномах над GF(p) и о действиях над ними при различных модулях р.

Перейдем к определению кольца полиномов над GF(p). Для того, чтобы вместо бесконечного множества полиномов всевозможных степеней получить конечное и при этом замкнутое множество, нужно задаться некоторым полиномом Q(х) степени k и использовать его так, как в числовом кольце используется число р, а именно - в качестве модуля, по которому приводится результат операции. Если элементами числового кольца являются числа от 0 до р-1, т.е. остатки от деления произвольного целого числа на р, то элементами кольца полиномов будут остатки от деления произвольных полиномов высоких степеней на полиномиальный модуль Q(х). Зададимся полиномом второй степени над GF(2)

Множество остатков от деления на Q(х) должно содержать все полиномы степени меньше двух, так как любой полином более высокой степени будет делиться на Q(X) с остатком или без него. В данном случае множество остатков определяется легко: М = {0, 1, х, х1}. Используя этот список, составим таблицы Кэли для сложения и умножения по модулю Q(X) (табл. 7.7 и 7.8).

Таблица 7.7

0 1 x x1
0 0 1 x x1
1 1 0 x1 x
x x x1 0 1
x1 x1 x 1 0

Таблица 7.8

0 1 x x1
0 0 0 0 0
1 0 1 x x1
x 0 x 1 x1
x1 0 x1 x1 0

Исследование таблиц показывает, что по сложению получается абелева группа, а по умножению группа не получается, так как в последней строке таблицы 9 нет единицы, иначе говоря, для х1 нет обратного элемента. В числовом кольце подобный результат получался при составном числе р, а здесь причина состоит в том, что принятый нами полиномиальный модуль разлагается на сомножители:

Q(х) = х2 1 = (х 1)(х 1).

Для получения поля полиномов над GF(2) нужно взять в качестве модуля Q(х) не разлагающийся на сомножители, т.е. неприводимый полином, например

Q(х) = х2 х 1.

Множество остатков будет таким же, но группа теперь будет получаться не только по сложению, но и по умножению (табл.7.9).

Таблица 7.9

0 1 х х1
0 0 0 0 0
1 0 0 х х1
х 0 х х1 1
х1 0 х1 1 х

Аналогично получаются кольца и поля полиномов над GF(p) при других р и при различных степенях полиномиального модуля вычетов.

Для прикладных теорий очень важно, что множеству полиномов, образующих расширенное поле Галуа GF(pk), изоморфно поле р -ичных чисел длиной до k разрядов по операциям поразрядное сложение и поразрядное умножение по mod p.

Степени фиктивной переменной х при этом заменяются степенями основания системы счисления. иначе говоря, любому полиному из GF(рk) однозначно соответствует р -ичное число, цифры которого равны соответствующим коэффициентам полинома. Например: полиному

2х5 х4 2 над GF(3) соответствует троичное число 210002.

Эта простая связь между алгебраическим выражением и позиционным числом позволяет описывать формулами самые различные преобразования цифровых кодов. Например, сдвиг влево на два разряда с приписыванием справа двух нулей выражается умножением на х2.

Сложение, умножение и деление полиномов над GF(p) можно заменить операциями над числами. Например при р = 2 умножение и деление цифровых кодов по правилам, определенным для полиномов дает результаты, не сводимые к обычному сложению и умножению чисел: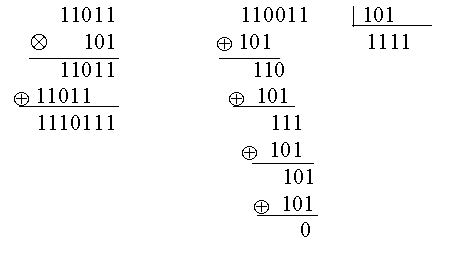

В приведенных здесь примерах обычные операции (при переводе в десятичную систему) давали бы 275 = 135 вместо 119 (1110111) и 51:5 = 10 1/5 вместо 15 (1111).

Содержание

Hosted by uCoz