5. Функции и отношения (лекция 5)

Из предыдущей лекции мы узнали, что функцией называется бинарное соответствие А ® В (т.е. из А и В), у которого во всей области определения обеспечивается однозначность образа в В. Кроме того, мы установили, что отображение, сюръекция и биекция представляют разновидности функции. Введем некоторые специальные понятия и термины, связанные с функциями.

Аргументом функции называется обобщенный символ элемента из области отправления соответствия. Если, например, область отправления содержит элементы а1, а2, а3,…, то символ а без индекса и есть аргумент. Подставляя различные буквы аi, можно задавать разные значения аргумента.

Значением функции называется элемент из области прибытия соответствия, который является образом соответствующего значения аргумента. В общем виде функцию одного аргумента можно записать в виде равенства

b = f(a),

где b – значение функции, а – аргумент, f – символ функциональной связи.

Один аргумент имеет одноместная функция, представляющая бинарное соответствие А ® В или Примеры одноместных функций:

Y = 5X; Y = X3; Y = lgX.

Двухместной функцией называется тернарное соответствие, устанавливающее связь вида или . Здесь значение функции определяется значениями двух аргументов, принадлежащих, возможно, двум разным множествам. Примеры двухместных функций:

Z = X+2Y; Z = XY.

Аналогично этому трехместная функция или функция трех аргументов задает связь вида , а n –местная функция, представляющая n-1 –арное соответствие задает связь вида .

Возникает вопрос: а могут ли существовать нуль-местные функции и унарные соответствия? Согласно определения у таких соответствий область отправления должна быть пуста, но в то же время образ (значение функции) должен определяться однозначно. Если такое соответствие можно представить состоящим из пар вида ( , b1), ( , b2), …, то, чтобы соответствие было функцией, нужно выбрать только одну такую пару, и тем самым обеспечить однозначность образа. Мы приходим к выводу, что нуль-местной функцией может быть только константа.

Заметим, что даже при большом числе аргументов, влияние некоторых из них на значение функции может отсутствовать (так называемые несущественные переменные), вследствие чего в некоторых задачах константа может быть определена, как многоместная функция.

Если одноместная функция f1 такова, что b = f1(a) и если мы считаем ее прямой функцией, то функция f2 такая, что a = f2(b), будет обратной к f1, или ее кофункцией. Ее можно обозначить f –1. Образы и прообразы меняются местами, поэтому для существования обратной функции необходимо, чтобы прямая функция была одноместной и была инъекцией, т.е. обеспечивала однозначность прообраза. Пример:

Y = f(X) = X3 – прямая, – обратная.

Для квадратичной функции Y = X2 обратная функция не существует, если не ограничить область определения условием , или если не заменить так называемую “четную” функцию “нечетной” функцией Y = X2 signX (квадрат Х со знаком Х). Не имеют обратных функций все двухместные и многоместные функции.

Возьмем две функции: b = f1(a) и c = f2(b). Образуем с их помощью третью функцию c = f2[f1(a)] = f3(a). Функция f3 называется композицией или подстановкой функций f1 и f2 и в общем виде может быть записана с помощью знака композиции

(f1 подставляется в f2). Подразумевается, что сперва выполняется действие f1, результат которого используется в f2. Возможны, хотя и не всегда, многократные подстановки

.

Когда более сложную функцию заменяют композицией более простых функций, то это называется декомпозицией. Благоприятные возможности для осуществления всевозможных композиций и декомпозиций получаются, если области определения всех функций представляют одно и то же множество, например: множество действительных чисел. В этом случае допустимы любые подстановки в любом порядке. Функции, получаемые путем композиции, декомпозиции и переименования аргументов, называются суперпозициями, а выражение, описывающее суперпозицию называется формулой.

Перейдем к способам задания функций. Мы знаем, что имеется два способа задания множеств: список и указание порождающей процедуры. Так как функция в ее формальном определении - всего лишь разновидность множества, то и для функций должны иметься аналогичные способы.

Табличное задание функции представляет соединение двух списков, где с каждым значением аргумента (или с каждым значением энки аргументов) сопоставляется одно определенное значение функции. Конечно, таблицу можно использовать только при небольшой мощности области определения функции. При увеличении числа аргументов или числа их возможных значений размер таблицы быстро растет. Тем не менее, в теории цифровых электронных устройств таблицы применяются очень широко.

В континуальной математике таблицы часто заменяют графиками, которые очень компактны и создают запоминающиеся зрительные образы функций.

Аналитическое задание функций использует формулы, в которых некоторая произвольная функция описывается композицией небольшого числа хорошо известных функций.

Рекурсивное определение функций представляет конструктивное развитие аналитического задания и применяется в тех случаях, когда аналитическое задание невозможно. Рекурсивное определение состоит из двух частей: входной и циклической.

Входная часть прямо задает значение функции на каком-нибудь одном значении аргумента. Эта часть рекурсии аналогична табличному заданию, только таблица здесь состоит из единственной строки. Обычно во входной части рекурсии функция определяется на значении аргумента, которое в списке находилось бы на первом месте, например: 0 или 1.

В циклической части указывается формула, по которой можно определить значение функции в следующей строке таблицы, если бы такая таблица существовала. В формуле значение функции определяется через композицию самой определяемой функции и одной или нескольких других функций, которые должны допускать аналитическое задание. Рекурсивным путем определяется, например функция факториала:

-входная часть рекурсии: 0! = 1;

-циклическая часть: х! = (х – 1)!х.

Пользуясь этим определением можно шаг за шагом вычислить значение факториала для некоторой заданной величины аргумента, т.е. как бы построить таблицу этой функции от нуля до заданной строки.

Рекурсивные определения в математике широко используются, когда приходится строго задавать не только не поддающиеся аналитическому описанию функции, но и различные множества. Например, считая известными функцию “константа 0” и функцию инкремента х+1, можно дать рекурсивное определение множества натуральных чисел с нулем:

-входная часть: х0 = 0;

-циклическая часть: хт+1 = хт+1.

Отношением R (от слова Relation), является частным случаем соответствия, когда область отправления и область прибытия представляют одно и то же множество. Примером отношения на множестве чисел является известное соответствие a > b; a, b N. Это отношение бинарно, так как связывает два элемента. В общем случае n-арное отношение определяется, как R An, но наибольший практический интерес представляют именно бинарные отношения.

Можно задавать отношения такими же таблицами, какие мы использовали для других соответствий. Только теперь таблицы обязательно будут квадратными, так как область отправления область прибытия равны. В таблице 5.1 показан пример отношения a < b на множестве {1, 2, 3, 4}. Расположение строк и столбцов таблицы является произвольным, так как для множеств порядок не имеет значения. Естественный порядок принят только из соображений удобства.

Таблица 5.1

 

1

2

3

4

1

  

1

1

1

2

    

1

1

3

      

1

4

        

Таблица 5.2

 

1

2

3

4

1

1

      

2

  

1

    

3

    

1

  

4

      

1

В таблице 5.2 показано отношение равенства на том же множестве. Это отношение обозначается R =idA и часто называется диагональю множества А.

Если отношение обеспечивает единственность образа для каждого элемента из области определения, то оно является функцией, и его можно использовать для каждого элемента из области определения, именно, как функцию, т.е. различать аргумент и значение функции и т.д. Связь между понятиями функции и отношения поясняет диаграмма Эйлера-Венна на рис. 5.1.

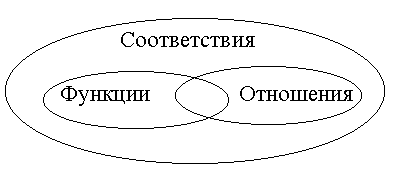
Рис. 5.1.

Формально любое соответствие можно представить как отношение, если объединить все участвующие в определении задачи множества в одно универсальное множество. Именно в этом смысле используют термин “отношение” в математической литературе. Мы будем все-таки избегать этого ненужного смешения терминов.

Несмотря на то, что термины “функция” и “отношение” могут в равной степени относиться к одному и тому же объекту, вкладываемый в них смысл различен. Когда говорят о функции, то подразумевают некоторое движение от причины к следствию. При этом наличие связи между элементами области отправления и области прибытия не вызывает сомнения, требуется тллько установить характер этой связи, показать характер поведения значений функции при изменении значений аргументов. Когда же говорят об отношении, то наоборот, характер связи известен, он запечатлен в названии отношения. Требуется только установить, для каких пар (прообраз-образ) данная связь существует, а для каких – нет. По-разному определяется и арность. Число мест функции на единицу меньше, чем арность отношения. В частности, бинарное отношение может являться только одноместной функцией.

Содержание

Hosted by uCoz