4.
Соответствия (лекция 4)Соответствием называется наиболее общий вид связи между элементами одного или нескольких множеств. Формально соответствие определяется, как некоторое подмножество декартова произведения множеств. Возьмем два множества:
A = {a, b, c, d, e} и B ={1, 2, 3, 4}. Их декартово произведение будет состоять из двадцати пар, состоящих из одной буквы и одной цифры. Возьмем подмножество этого произведенияC1 = {(a, 1), (b, 2), (c, 4), (d, 3), (e, 1)}.
Этот список полностью описывает определенное соответствие “из
A в B”. Выбирая другие подмножества
будем получать другие
соответствия. К понятию “соответствие” можно
свести любую связь между элементами множеств,
ввиду чего данное понятие является одним из
основных в математике.
Соответствия вида
A ® B называются бинарными, так как связывают между собой два множества. Соответствие вида
D или 
называется
тернарным, так как связывает три множества.
Мы пока ограничимся рассмотрением бинарных
соответствий.
Конкретное содержание конечных соответствий можно задавать с помощью таблиц. Таблица 4.1 описывает определенное выше соответствие С
1.Таблица 4.1
1 |
2 |
3 |
4 |
|
a |
1 |
|||
b |
1 |
|||
c |
1 |
|||
d |
1 |
|||
e |
1 |
Множество
букв будем называть областью отправления соответствия, а множество цифр – областью прибытия. Для удобства словесных формулировок введем термины: образ и прообраз. В данном примере буква а является прообразом во множестве А элемента 1 множества В. И наоборот, цифра 1 является образом в В элемента а.В таблице 4.1 образ определен для каждого прообраза. Такие соответствия называются всюду определенными. У них область определения совпадает с областью отправления:
dom C = A. Кроме того, образ здесь всюду определен однозначно. Соответствия, обладающие этим свойством, называются функциональными, или просто функциями. В данном случае мы имеем всюду определенную функцию, т.е. отображение.В таблице 4.2 представлено соответствие, у которого область определения меньше области отправления, т.е. у которого
. В то же время у каждого из
прообразов, составляющих область определения,
имеется однозначно определенный образ в В.
Такие соответствия называются частичными
функциями.
Таблица 4.2
|
Таблица 4.3
|
Таблица 4.4
|
У соответствий в таблицах 4.1 и 4.2 для каждого из элементов области прибытия В имеется прообраз в А. Такие соответствия называются сюръективными соответствиями, а если они к тому же являются функциями (неважно, полностью определенными или частичными), то их называют сюръекциями. В таблицах 4.1 и 4.2 показаны сюръекции.
В табл. 4.3 показана полностью определенная функция, которая не является сюръекцией, так как область ее значений меньше области прибытия
.Если соответствие не обеспечивает однозначности в области прибытия, то оно является не функцией, а соответствием более общего вида. При этом оно может быть соответствием полностью определенным или частичным, сюръективным или не сюръективным.
В таблице 4.4 представлено частичное и не сюръективное соответствие, не являющееся функцией, так как для элемента а определено два образа: 1 и 3. Но у этого соответствия для каждого из элементов области значений прообраз определен однозначно. Соответствия, обладающее этим последним свойством, называются инъективными соответствиями, а если это – функции, то простоинъекциями. Соответствия из таблиц 4.1 и 4.3 не инъективны, а в таблице 4.2 показана инъекция.
Уже было сказано, что всюду определенные функции можно называть отображениями. При этом отличают отображение на (сюръективное) и отображение в (не сюръективное).
Взаимно - однозначным отображением или биекцией называется функция, которая является отображением, сюръекцией и инъекцией. Биекция возможна только между равномощными множествами. Этим пользуются для доказательства равномощности множеств: достаточно доказать существование взаимно - однозначного отображения между их элементами.
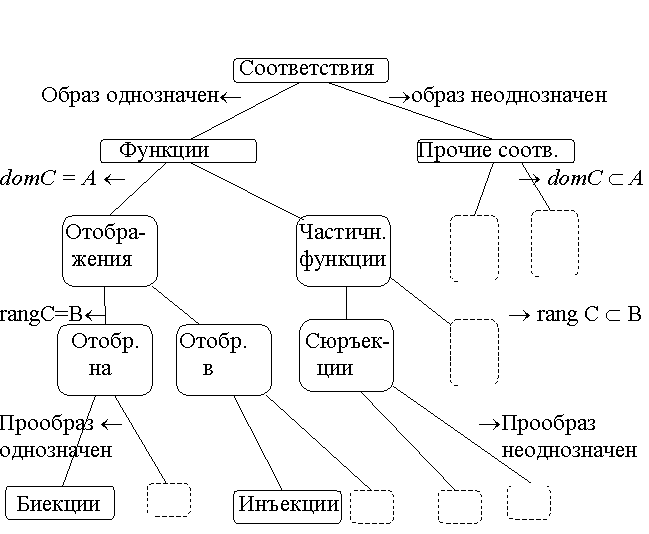
На рис. 4.1 показана классификация соответствий по четырем признакам:
Рис. 4.1
