 .
.3. Мощность множеств (лекция 3)
Мощность множества – это число его элементов, которое может быть только целым. Это – единственная количественная характеристика, которой в полной мере оперирует теория множеств. Для обозначения мощности символ множества заключают в прямые скобки или используют отдельный символ, например
|A| = n. При небольших величинах мощности она определяется простым подсчетом или по подходящей формуле, но для бесконечных множеств оценка их мощности может быть сделана только путем сравнения с мощностью других, достаточно известных множеств. Иначе говоря, для того, чтобы охарактеризовать мощность бесконечного множества, необходимо отыскать известное равномощное множество.Счётным множеством называется любое множество, равномощное множеству
N натуральных чисел. Счётное множество – это такое множество, элементы которого могут быть занумерованы натуральными числами так, чтобы каждый элемент получил свой особенный номер. Если подобная нумерация невозможна (номеров меньше, чем это необходимо), то множество называется несчетным.При исследовании бесконечных множеств обнаруживаются неожиданные факты. Оказывается, их мощности могут иметь только дискретные значения, называемые “кардинальными числами”. Одно из кардинальных чисел
Если объединять конечные множества, у которых ни один элемент не совпадает, то мощность объединения определяется суммой их мощностей. При
|A1| = n1, |A2| = n2, ... получим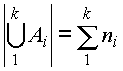 .
.
При объединении конечных множеств, которые могут пересекаться, результирующая мощность определяется более сложным путем. Для этого приходится использовать специальные прием, который в комбинаторике называется “методом включения и исключения”. Мощность объединения двух множеств определяется по формуле
![]() .
.
Мощность пересечения вычитается, чтобы не учитывались дважды элементы, принадлежащие обоим объединяемым множествам. Аналогично, при объединении трех множеств
![]() .
.
Последний член возвращает те элементы, которые из-за принадлежности ко всем трем множествам были исключены трижды. Количество включений элементов со знаком “плюс” или “минус” в результирующую сумму поясняет рисунок 3.1.
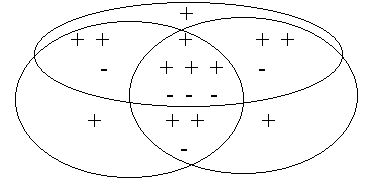
Рис. 3.1
Рассуждая аналогичным образом, можно вывести общий вид формулы для мощности объединения
n множеств
Эта формула в дальнейшем пригодится для решения комбинаторных задач. В одном частном случае, а именно, когда объединяемые множества не пересекаются, все члены в правой части этой формулы, кроме первого, равны нулю и мы возвращаемся к ранее определенной простой формуле мощности объединения конечных множеств.
Объединение бесконечных множеств дает другие результаты. Мощность объединения конечного числа
k счетных множеств равна (теорема Т1):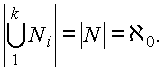
Докажем теорему Т1. Пронумеруем первые элементы всех объединяемых множеств. Поскольку
k конечно, это вполне выполнимо. Затем присвоим следующие номера вторым элементам всех множеств и т.д. Теоретически мы таким путем можем пронумеровать все элементы всех множеств. А это означает, что объединение конечного числа счетных множеств счетно. Такой же результат получим для объединения счетного числа конечных множеств (теорема Т2):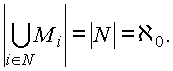
Доказательство делается аналогично предыдущему. Нумеруем все элементы первого множества (ведь оно конечно!), затем второго и т.д. Теоретически это достижимо, значит, теорема Т2 доказана.
Несколько более сложным путем доказывается, что объединение счетного числа счетных множеств тоже равно счетному множеству(теорема Т3):
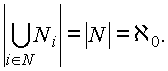
![]()
Для доказательства теоремы Т3 рассмотрим декартову степень счетного множества
![]()
Из каких пар состоит эта степень? начнем перечислять их в порядке возрастания номеров элементов
(a1,a1),(a1,a2),(a2,a1),(a1,a3),(a2,a2),(a3,a1),(a1,a4),(a2,a3),(a3,a2),...
В первой паре сумма номеров элементов равна двум, во второй и третьей парах она равна трем, затем идут три пары с суммой номеров, равной четырем, и т.д. В общем виде можно разбить все множество таких пар на классы
Ck = {(ai, aj)| i + j = k + 1}; k I N.
Число пар в каждом классе равно
k – конечному, хотя и неограниченно возрастающему числу. Это значит, что мы свели задачу к случаю теоремы Т2, т.е. к объединению бесконечного числа конечных множеств. Пока что мы доказали лишь то, что декартово произведение двух счетных множеств счетно:![]()
Приступим теперь к доказательству Т3. Изобразим множество классов декартова произведения в виде треугольного массива, заменяя каждую пару одной буквой с двойным индексом (номер класса и номер пары в классе):
p11 |
|||
p21 |
p22 |
||
p31 |
p32 |
p33 |
|
... |
... |
... |
... |
Далее построим второй такой же массив
q11 |
|||
q21 |
q22 |
||
q31 |
q32 |
q33 |
|
... |
... |
... |
... |
Повернем второй массив вокруг диагонали и соединим оба массива в один прямоугольный массив, бесконечно продолжающийся вправо и вниз:
p11 |
q11 |
q21 |
q31 |
... |
p21 |
p22 |
q22 |
q32 |
... |
p31 |
p32 |
p33 |
q33 |
... |
... |
... |
... |
... |
... |
Поскольку мы объединили два счетных множества (число множеств конечно!), то в силу теоремы Т1 получили счетное множество. В то же время структура построенного нами прямоугольного массива точно соответствует объединению счетного числа счетных множеств, ведь каждая строка представляет одно такое множество! Теорема Т3 доказана.
Счетное множество оказалось своеобразной матрешкой, бесконечное число раз содержащей саму себя. Из-за этого парадокса возникает сомнение в возможности существования множеств с кардинальными числами более высокого порядка. Чтобы убедиться в их существовании докажем, что множество
действительных чисел отрезка (0, 1) несчетно.Для доказательства применим открытый Кантором “диагональный метод”, представляющий специальный вариант доказательства “от противного”. Допустим, что действительные числа от нуля до единицы образуют счетное множество. Тогда они могут быть пронумерованы. Номер должен представлять бесконечную дробь
ai = 0,a i1a i2a i3..., где a ij – обычные, например десятичные цифры. Выписав столбиком все эти дроби (разумеется, чисто умозрительно), получим массив, продолжающийся бесконечно вправо и внизa1 = 0,a 11a 12a 13 ...
a2 = 0,a 21a 22a 23 ...
a3 = 0,a 31a 32a 33 ...
... ... ... ... ... ...
Имея в виду полученный массив, составим бесконечную дробь
b = 0,b 1b 2b 3 ...
таким образом, чтобы
b1№a11, b2№a22, b3№a33 и т.д. такую дробь несомненно можно построить, причем не единственным способом, а во многих вариантах. Если наше первоначальное предположение было верным, то дробь b, представляющая одну из точек отрезка (0,1) должна была бы найтись среди чисел, образующих массив. Но это невозможно, так как от первой строки массива наша дробь отличается старшей цифрой дробной части, от второй строки – следующей цифрой и т. д. Итак, допущение было неверным и привело к противоречию. Кардинальные числа алеф-нуль и алеф-один связывает между собой так называемая континуум- гипотеза![]()