1. Множества и операции над ними (лекция 1)
Термины “множество” и “элемент множества” являются первичными, для них существует только интуитивное определение. У множества нет других свойств, кроме того, что оно должно состоять из целого числа элементов, а у элементов не должно быть других свойств, кроме способности образовывать множества. Мы будем обозначать множества заглавными, а элементы – строчными буквами. Элемент
a может быть связан с множеством A знаком принадлежности
или отрицания
принадлежности 
. Поворачивать эти
символы на 180о не разрешается.
Для задания множеств существует несколько способов, простейший из которых состоит в словесном описании характерного свойства множества или его элементов, например: “множество студентов в потоке” или “множество книг”. Этот способ является недостаточно строгим, так как множество не определяется, а только получает название. Опыт показал, что это нередко ведет к ошибкам и противоречиям, ведь придумать название можно и для такого множества, которое невозможно построить (“множество всех множеств”). Словесное описание сейчас применяют только к хорошо известным или очень простым множествам.
Множество может быть задано списком, например:
Список показывает из скольких элементов, и каких именно состоит множество. Общепринято список элементов заключать в фигурные скобки. Расположение элементов в списке может быть произвольным, но для удобства чтения предпочтительным является так называемый естественный порядок. С помощью списка можно задавать только множества, состоящие из небольшого числа элементов. Впрочем, некоторые бесконечные множества удается задавать оборванным списком. Так можно задать, например множество натуральных чисел и множество неотрицательных четных чисел:
Применение оборванных списков требует осторожности, так как не исключено их ошибочное понимание. В частности, в первом из приведенных выше списков можно увидеть ряд простых чисел: 1, 2, 3, 5, 7,
...Третий способ задания множеств состоит в указании порождающей процедуры. Вместо оборванного списка множества
Q можно написать
Смысл этой записи:
Q – множество, состоящее из элементов q. Любой элемент этого вида обладает характерным свойством, смысл которого разъясняется записью справа от вертикальной черты. В данном случае свойство элемента состоит в возможности его получения удвоением натурального числа, в том числе и нуля. Другие примеры записи порождающих процедур:
Элементами множеств могут быть не только числа, но и любые объекты: предметы и цвета, графические образы и произвольные абстрактные понятия. Единственное требование, которое всегда соблюдается: число элементов, составляющих множество должно быть целым. Множества могут быть элементами других множеств, например:
Здесь символы
B, C ,D в одном случае обозначают элементы, а в другом – множества.Не содержащее ни одного элемента множество называется пустым и обозначается знаком
Это понятие аналогично нулю в
арифметике. Два множества равны, когда они
состоят из одних и тех же элементов. Для
доказательства равенства A = B нужно установить, что каждый
элемент первого множества одновременно
принадлежит второму и наоборот.
Подмножеством
A множества B называется такое множество A, все элементы которого одновременно принадлежат B. Обратное условие не ставится. Подмножество связывает с множеством знак включения
(A входит в B). Знак
включения можно поворачивать: 
(B
покрывает или содержит A).
Собственным (строгим, истинным) подмножеством называется такое, что
и
в то же время 
. При этом его
можно обозначать знаком строгого включения 
. При несоблюдении одного из
указанных условий подмножество считается несобственным.
Пустое множество в качестве несобственного подмножества входит в любое множество и, следовательно, в любое подмножество. Выпишем все подмножества множества
A: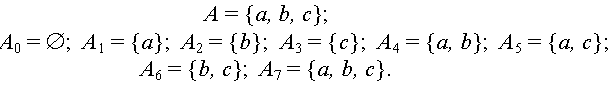
Всего оказалось восемь подмножеств, из них два несобственных:
A0 и A7.Над множествами можно выполнять четыре основные операции. Рассмотрим их.
Объединением множеств называется множество элементов, принадлежащих хотя бы одному из объединяемых множеств
Можно определить объединение по общему правилу указания порождающей процедуры:
Объединение является многоместной операцией, так как одновременно может объединяться любое число множеств:
Когда число объединяемых множеств велико, объединение можно представить в общем виде, используя один из следующих вариантов записи:
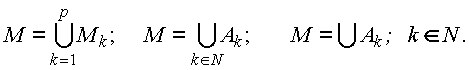
Пересечением множеств (взятием общей части) называется множество, элементы которого одновременно принадлежат обоим пересекаемым множествам. Например:
Можно определить пересечение как
Пересечение тоже многоместно:
Разностью
множеств
называется множество элементов, принадлежащих A, но не
принадлежащих B. Например:
Вообще
В отличие от объединения и пересечения разность – двухместная операция.
Дополнением
множества A называется множество всех элементов, принадлежащих некоторому универсальному
(всеобъемлющему) множеству U, но не принадлежащих A. Иначе говоря, дополнение – это разность 
. Смысл универсального
множества обычно понятен из условий задачи, но в
операцию дополнения оно в явном виде не входит, а
только подразумевается. Поэтому дополнение
считается одноместной операцией.
Все основные операции над множествами наглядно поясняются диаграммами Эйлера-Венна. Если элементы множества представить, как точки на плоскости, то сами множества будут представляться некоторыми областями, выделенными на плоскости (рис. 1.1)
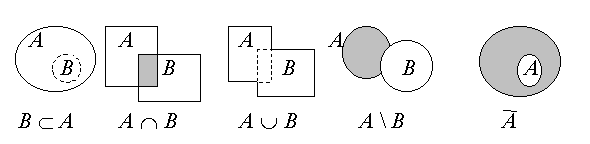
Рис. 1.1
Объединение и пересечение ассоциативны:
коммутативны:
пересечение дистрибутивно относительно объединения и разности:
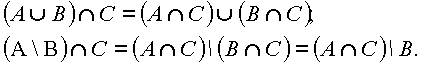
Видно, что свойства теоретико-множественных операций аналогичны свойствам операций обычной арифметики (сложение, умножение и вычитание), за исключением последнего равенства. Тем не менее, разница между теоретико-множественными и арифметическими операциями очень велика. Сравним, например:
или 
с
арифметическим сложением 1 + 1 = 2. Наиболее важные
приложения теории множеств относятся к задачам,
где количественные характеристики элементов
вообще не имеют значения.
