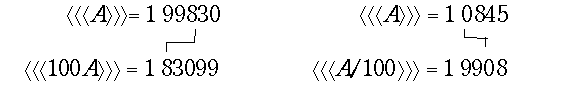19.
Контроль переполнения при сложении кодов. Сдвиги(
лекция 19)Переполнение разрядной сетки в любом случае является грубой ошибкой и непременно должно обнаруживаться аппаратными средствами. Проще всего контролируется переполнение при сложении прямых кодов. При сложении прямых кодов переносы в знаковый разряд вообще не должны происходить, поэтому возникновение такого переноса можно использовать как признак переполнения.
При сложении дополнительных или обратных кодов перенос в знаковый разряд сам по себе не является признаком переполнения. Для контроля переполнения здесь можно применить один из трех способов:
а) анализ
знаковых цифр операндов и результата операции. Обозначим знаковые цифры слагаемых B, C и суммы A соответственно b, c и a. Переполнение возможно только при одинаковом знаке слагаемых. Оно должно обнаруживаться получением неверного знака суммы, не совпадающего со знаком слагаемых. Признак (флаг) переполнения OF определяет логическая формула
Этот способ не может быть применен, в частности, при одноадресном сложении из-за невозможности одновременного чтения знаковых цифр обоих операндов;
б) контроль
с применением модифицированных кодов состоит в использовании двух знаковых цифр вместо одной. Общее число цифр в модифицированном коде получается равным n + 1. Так как сложение двух n - 1 - разрядных модулей не может дать сумму с более, чем с n -разрядным модулем, старшая из двух знаковых цифр всегда сохраняет правильное изображение знака. Младшая из знаковых цифр при переполнении инвертируется, следовательно, признаком переполнения является несовпадение знаковых цифр. Примеры сложения модифицированных дополнительных кодов (обозначения кодов такие же, как в предыдущей лекции, двойные угловые скобки означают дополнительный код):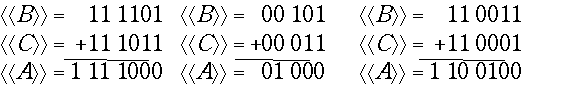
В первом примере переполнения нет, а во втором и третьем наблюдается переполнение. Выходящие из разрядной сетки цифры переносов из старшего знакового разряда (первый и третий примеры) игнорируются, как и вообще при сложении дополнительных кодов.
Для преобразования обычного кода в модифицированный, знаковая цифра операнда направляется сразу на два входа сумматора - в разряды с номерами
n - 1 и n. Сумматор соответственно должен иметь увеличенную разрядность. Обе знаковые цифры участвуют в сложении наряду с цифрами модуля (или дополнения), как это и должно быть при применении дополнительного или обратного кода. Примеры с обратным модифицированным кодом: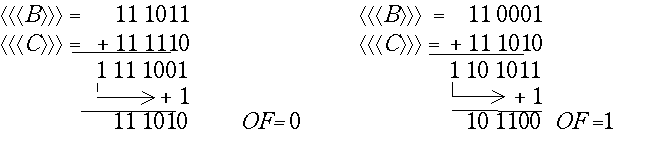
Логический признак переполнения при этом способе выражается как
;
в) контроль
по значению переносов CR[n - 1] (в знаковый разряд) и CR[n] (из знакового разряда). В принципе этот способ аналогичен предыдущему, но не требует увеличения разрядности сумматора и регистра-аккумулятора. Нужно только соединить цепи переносов сумматора с логической схемой, реализующей функцию
. На практике эти способы
применяются в неявной форме, флаг OF выставляется на основании
логического анализа ситуации.
Сдвиг двоичного числа влево на
k разрядов эквивалентен умножению его на
,
сдвиг вправо - делению на .
Крайние цифры при сдвиге теряются. Эти общие
положения справедливы для любых чисел и любых
кодов, но в деталях имеются отличия.
Необходимо различать сдвиг
кода и сдвиг арифметический. Сдвиг кода или логический сдвиг выполняется просто. Сдвигаются все цифры, освободившиеся разряды занимаются нулями.В арифметическом сдвиге знаковый разряд не участвует, он сохраняет свою прежнюю цифру. Таким образом, умножается или делится на
только модуль числа (или его
дополнение до 
). Крайние цифры
модуля теряются. Если число положительно, то
освободившиеся разряды занимаются нулями. Если
же оно отрицательно, то освободившиеся разряды
занимаются по-разному в зависимости от принятого
кода и от направления сдвига. Соответствующие
правила сведены в таблицу 4.1.
Таблица
4.1
Докажем необходимость именно такого выполнения арифметического сдвига над дополнительным и обратным кодами отрицательных чисел.
Сдвиг дополнительного кода на один разряд вправо, то есть деление дополнения модуля числа на два можно описать формулой
.
Первые два члена правой части равенства как раз дают верное изображение дополнения. Третий член означает нехватку единицы старшего разряда модуля. Чтобы скомпенсировать эту нехватку нужно, согласно таблице, вписать единицу в освободившийся слева разряд.
Следует иметь в виду, что величина А/2 представляется неточно: потеря младшей цифры кода, если это была единица, означает округление дополнения в меньшую сторону, а модуля числа - в большую. Пример:
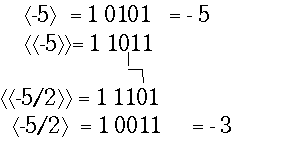
Соответствующая формула для обратного кода:
Здесь до верного кода опять недостает
и эта единица добавляется в
освободившийся разряд. Что касается излишка +1/2,
который нужно устранить, то он соответствует
вышедшей из разрядной сетки цифре. Если код до
сдвига оканчивался единицей, то ошибка
округления отсутствует. И наоборот, ошибка
возникает, если код до сдвига оканчивался нулем.
Дополнение при этом округляется в большую
сторону, а модуль числа - в меньшую. Аналогичные
рассуждения проделаем для сдвига влево.
Умножение отрицательного двоичного числа на 2, то
есть сдвиг его на один разряд влево в
дополнительном коде можно описать формулой:
.
Первая из единиц с весом
выдвигается из разрядной сетки модуля и
теряется, остается дополнение 2|A| до, что и
требовалось. Коррекция не нужна.
В обратном коде соответственно получится
.
Первый член формулы, как и в дополнительном коде, теряется. Но в младшем разряде обнаруживается нехватка единицы. Чтобы результат получился верным, необходимо в младший разряд при каждом сдвиге влево вписывать единицу.
Если сдвигаемое число представлено в модифицированном коде (дополнительном или обратном), то арифметический сдвиг выполняется особенным образом и называется модифицированным сдвигом. Старшая из знаковых цифр остается на прежнем месте, а младшая участвует в сдвиге вместе с цифрами дополнения. Такая организация сдвига позволяет сохранить верный знак числа и восстановить правильное представление числа. Пример арифметического сдвига вправо:
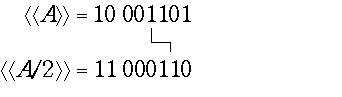
Расположение запятой не влияет на правила выполнения сдвигов. Над правильными или неправильными дробями сдвиги выполняются точно так же, как над целыми числами. При других основаниях системы счисления сдвиги выполняются аналогично, только вместо единицы для заполнения освободившихся разрядов берется старшая из допустимых цифр. Примеры арифметического сдвига десятичных дробей:
